2. Umlaufbahn und Parameter von GPS-Satelliten

Zu dem GPS-System im Weltall zählen mindestens 24 Satelliten. Die GPS-Satelliten befinden sich in einer Höhe von 20200 km über der Erde und laufen auf einer nahezu kreisförmigen Bahn im mittleren Erdorbit.

Ein GPS-Satellit.

Die Umlaufgeschwindigkeit und die Umlaufzeit eines GPS-Satelliten lässt sich aus der Information des Abstands zwischen Erde und Satellit herleiten. Auf den Satelliten, der eine kreisförmige Umlaufbahn um die Erde verfolgt, wirken die Gravitationskraft

F_{G} = \frac{γ \cdot M \cdot m}{r^{2}}

und die Zentrifugalkraft

F_{Z} = \frac{M \cdot v^{2}}{r}

welche sich gegenseitig ausgleichen, sodass der Satellit eine kreisende Bewegung um die Erde machen kann.

Es ist

γ=6,67·10^-11 m³(kg s²)^-1 die Gravitationskonstante,
M=5,976·10²⁴ kg die Masse der Erde,
m die Masse des Satelliten,
r der Abstand zwischen Erdmittelpunkt und Satellit.

Der Erdradius beträgt r_E=6371 km .

Aufgabe 1
Leiten Sie aus dem Ansatz F_G=F_Z eine Gleichung für die Geschwindigkeit v des Satelliten in Abhängigkeit von der Entfernung zum Erdmittelpunkt (bzw. des Radius des Kreises) her.

Lösung ↓

Aus dem Ansatz F_G=F_Z folgt nach Umformungen die Gleichung zur Bestimmung der Geschwindigkeit v auf der Kreisbahn

v = \sqrt{\frac{γ \cdot M}{r}}

r=26571 km ist der Abstand vom Erdmittelpunkt zum Satelliten.

Aufgabe 2
Bestimmen Sie anschließend die Geschwindigkeit eines GPS-Satelliten.

Lösung ↓

Aufgabe 3
Wie lange braucht ein GPS-Satellit für einen Erdumlauf?

Lösung ↓

Die Umlaufzeit T einer Kreisbahn ergibt sich aus dem Quotienten des Kreisumfangs r und der Geschwindigkeit v:

T = \frac{2 π \cdot r}{v}

r=26571 km ist der Abstand vom Erdmittelpunkt bis zum Satelliten.
Die Zeit, die ein GPS-Satellit für einen Erdumlauf benötigt lässt sich mit dieser Gleichung berechnen. Es wird: T=43104 s oder 11 Stunden und 58 Minuten.

Aufgabe 4
Geben Sie eine von der Geschwindigkeit v unabhängige Formel zur Bestimmung der Umlaufzeit T an.

Lösung ↓

Um die Umlaufzeit einer Kreisbahn ohne die Geschwindigkeit auszudrücken, kann man die Gleichung der Geschwindigkeit in die der Umlaufzeit einsetzen. Es ergibt sich:

T = 2 π \sqrt{\frac{r^{3}}{γ \cdot M}}

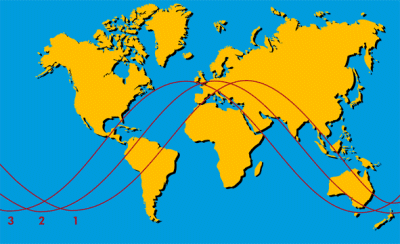
Ein GPS-Satellit umrundet die Erde also in rund 12 Stunden, d.h. zwei mal pro Tag. Jedoch macht gerade die geringe Abweichung von ca. zwei Minuten pro Umlauf aus, dass der gleiche GPS-Satellit jeden Tag etwa vier Minuten früher über der gleichen Position steht. Das bedeutet, dass die Satellitenspur täglich um ca. 1° westwärts wandert. Die Spur ist der geometrische Ort aller Punkte auf der Erdoberfläche, die zu irgendeinem Zeitpunkt auf der ständig wandernden Verbindungslinie zwischen Satellit und Erdmittelpunkt liegen. Eine solche Spurverschiebung ist in der folgenden Abbildung zu erkennen.

Spurverschiebung

Satellitennavigation mit GPS

2. Umlaufbahn und Parameter von GPS-Satelliten