2. Einführung in die mathematischen Methoden
Die Häufigkeitsverteilung
Bei der automatischen Klassifizierung von Satellitendaten werden erweiterte statistische Methoden genutzt. Dieses zweite Kapitel gibt eine kurze Einführung in die verwendeten mathematischen Methoden.
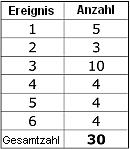
Wenn Sie einen Würfel nehmen, ihn 30 mal werfen und dabei aufschreiben, wie oft Sie welche Zahl gewürfelt haben, könnten Sie einen Datensatz wie den folgenden erhalten.
Mit einem Würfel kann man nur die Ergebnisse 1, 2, 3, 4, 5 oder 6 erhalten, also nur diskrete Werte. Daher spricht man hier von diskreten Daten. Die Zahlen 1, 2, 3, 4, 5 und 6 bilden den Definitionsbereich eines Würfels; d.h. es sind die einzigen Werte, die mit einem normalen quadratischen Würfel erzielt werden können. Zählt man, wie oft jede Zahl in dem Datensatz auftritt, erhält man eine Tabelle wie die unten stehende.
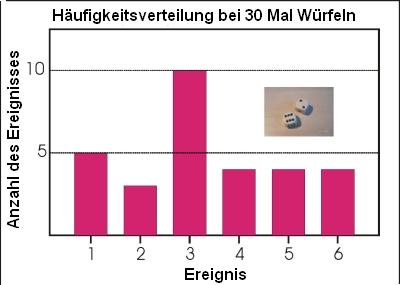
Dieses Ergebnis können Sie zum Beispiel mit einem Tabellen- kalkulationsprogramm graphisch darstellen, wie hier gezeigt. Hier ist eine Häufigkeitsverteilung diskreter Daten dargestellt:
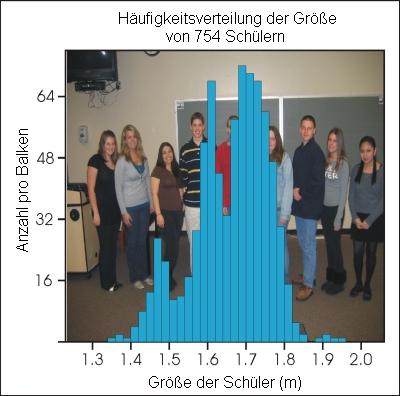
Wie geht man vor, wenn es sich um kontinuierliche Daten handelt, also um Daten, die jeden Wert innerhalb eines Wertebereiches annehmen können, wie beispielsweise die Körpergröße verschiedener Menschen? Wie erstellt man eine Häufigkeitsverteilung für solche Daten?
Sehen Sie sich beispielhafte Daten an und finden Sie den Maximal- und den Minimalwert, um den Wertebereich zu erhalten, den die Daten abdecken. Entscheiden Sie, wie viele Balken die Häufigkeitsverteilung haben soll und teilen Sie den Wertebereich durch die Zahl der Balken. Stellen Sie nun für ihre Daten fest, wie viele Werte im Bereich jedes Balken liegen. Sobald Sie damit fertig sind, können Sie ein Histogramm zeichnen.
Frage:
Was sagt die Häufigkeitsverteilung über ihre Daten aus?
Aufgaben, Lerneinheiten und Antworten