2. Einführung in die mathematischen Methoden

Wertmaße

Manchmal möchte man einen einzigen Wert zur Verfügung haben, der für die Daten steht. Welchen Wert nutzt man am Besten?

Es gibt drei Werte, unter denen man wählen kann:

  • der Mittelwert
  • der Modalwert
  • der Medianwert

Liegen mehrere Beobachtungen { x 1 , x 2 , x 3 , …, x i , …, x n } vor, wobei jedes x i eine einzelne Beobachtung ist, dann ergibt sich der Mittelwert aus der folgenden Gleichung:

X ¯ = ( x 1 + x 2 + x 3 +...+ x n ) n = ∑ i=1 n x i n

Der Mittelwert einer Stichprobe wird mit dem Symbol x ¯ dargestellt, genannt 'x quer'. Diese Gleichung kann man als Summe von n einzelnen Beobachtungen geteilt durch die Anzahl der Beobachtungen bezeichnen. Eine Abkürzung für die Summe von Beobachtungen ist der griechische Buchstabe Σ (Sigma), wobei ein Buchstabe unterhalb des Symbols den Wert angibt, der sich beim Addieren verändert, in diesem Beispiel die Laufzahl i in der Folge { x 1 , x 2 , x 3 , …, x i , …, x n } . Die Zahlenwerte unter und über dem Sigma zeigen den ersten und den letzten Wert an, auf den sich die Laufzahl bezieht, das heißt also:

∑ i = 1 4 x i  =  x 1  +  x 2  +  x 3  +  x 4

Anders ist es bei den Daten einer Häufigkeitsverteilung. Jede Klasse der Häufigkeitsverteilung gibt die Anzahl des Auftretens dieses Wertes an oder die Zahl der Beobachtungen in dieser Klasse. Der Mittelwert wird als Summe des Produktes der Klassenwerte mal der Klassenzahl geteilt durch die Summe der Anzahl pro Klasse berechnet.

Daher gilt für gruppierte Daten:

x ¯  =  ∑ k i · v i ∑ k i

wobei k i und v i für den Zählerstand im Histogramm und den Wert der Klasse i stehen.

Der Modalwert ist der Wert, der in einem Datensatz am Häufigsten auftaucht, während der Median die obere und die untere Hälfte der Werte in einer Stichprobe voneinander abgrenzt. Es handelt sich dabei um den mittleren Wert zwischen den höchsten und den niedrigsten Werten in einem Datensatz. Beinhaltet der Datensatz eine gerade Anzahl an Werten, wie es zum Beispiel bei einem Würfel der Fall ist, so liegt der Median auch in der Mitte, d.h. beim Würfel würde er 3,5 betragen.




Beispiel: Nehmen wir an, wir haben folgenden Datensatz als Ergebnis eines Würfelexperiments erhalten:
1, 3, 5, 2, 4, 4, 1, 6, 1

Der Modalwert dieses Datensatzes ist 1, da dieser Wert dreimal auftritt, während alle anderen möglichen Werte nur ein- oder zweimal vorkommen.

Der Median beträgt bei diesem Experiment 1+62=3,5.

Der Mittelwert ist X=1+3+5+2+4+4+1+6+19=279=3.

Zoom Sign
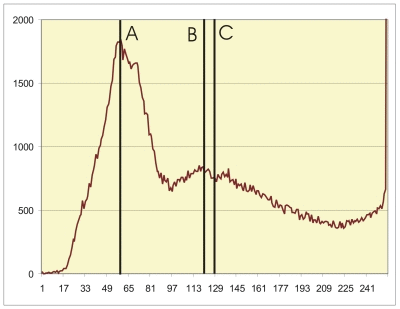
Sample distribution
Verteilung von Stichproben

Fragen

  1. In dem Histogramm oben sind Mittelwert, Median und Modalwert als Linien eingezeichnet und mit den Zahlen (A), (B) und (C) beschriftet. Welche Linie stellt den Mittelwert dar, welche Modalwert und Median?

  2. Wir haben bereits vom Mittelwert der Stichprobe, x ¯ gesprochen. Was ist der Erwartungswert µ? Unterscheidet sich der Erwartungwert von dem Mittelwert der Stichprobe und wenn ja, warum? Hinweis - Sie sollten sich die Definitionen von Stichprobe und Population in einem Lexikon ansehen.

Aufgaben, Lerneinheiten und Antworten