2. Einführung in die mathematischen Methoden
Die mehrdimensionale Häufigkeitsverteilung
Bisher haben wir nur Daten in einer Dimension berücksichtigt. Aber wie geht behandelt man Daten in mehreren Dimensionen, und wie werden sie dargestellt?
Zweidimensionale Daten lassen sich mit einer 2D-Häufigkeitsverteilung betrachten.
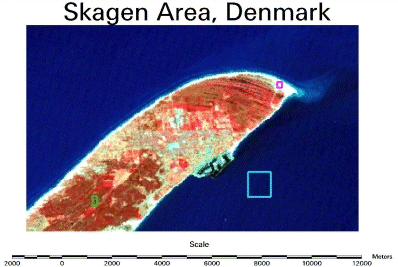
Bildquelle: USGS
Um Ihre eigenen 2D-Häufigkeitsverteilungen oder Streudiagramme zu zeichnen, benutzen Sie die Daten aus der Datei skagensub.asc und importieren Sie sie in ein Tabellenkalkulationsprogramm. Die ersten beiden Spalten in dieser Datei geben Rechts- und Hochwert der Pixel an. Jedes Pixel ist 20 Meter × 20 Meter groß, sodass man ihre Lage auf der Karte ausfindig machen kann. Die anderen vier Daten sind die Werte der spektralen Banden des Thematic Mapper an diesem Punkt. Tragen Sie jeden Wert gegen jeden anderen Wert auf. Zwei der sich dabei ergebenden 2D-Häufigkeitsverteilungen oder Streudiagramme sollten wie die hier dargestellten aussehen.
Man erkennt, dass bei größeren Werten für Bande 1 auch größere Werte für Bande 2 auftreten, während hohe Werte in Bande 4 nicht unbedingt größere Werte für Bande 1 zur Folge haben. Die Daten der Banden 1 und 2 hängen also miteinander zusammen, oder statistisch gesprochen, sie korrelieren. Korrelationen werden auf der folgenden Seite näher untersucht.
Mit den Daten für vier Banden kann man insgesamt sechs Streudiagramme erstellen. Probieren Sie das in Ihrem Tabellenblatt aus.
Wenn man Daten zu n Banden hat, wie viele Streudiagramme könnte man dann zeichnen? Die Antwort lautet:
Hat man die Daten von sieben Banden, sagen dann die Streudiagramme alles über die Daten aus, was man über sie wissen möchte? Nicht wirklich. Zeichnen Sie Histogramme für jede Bande; Sie werden erkennen, dass sie nicht so viele Aussagen über die Beziehungen zwischen den Werten zweier Banden ermöglichen wie die Streudiagramme. Auch anhand eines Streudiagrammes, das den Zusammenhang zwischen zwei Banden darstellt, erfährt man nicht alles, was man über die Abhängigkeiten zwischen den Daten aller Banden wissen könnte, wenn in den Bilddaten drei oder mehr Banden vorkommen.
Es ist ziemlich schwierig, höherdimensionale Daten nachzuvollziehen. Daher bietet es sich an, aus den Daten abgeleitete Statistiken zu nutzen, um zu verstehen, wie die Daten miteinander zusammenhängen. Im Folgenden wird vorgestellt, wie solche Statistiken gewonnen werden.
Wir haben gelernt:
Streudiagramme zeigen für die Versuchsflächen unterschiedliche Strukturen.
Möglicherweise ist es sinnvoll, etwas mehr in die Tiefe zu gehen, um eine
(halb-)automatisierte Klassifizierungsmethode zu finden.

