2. Einführung in die mathematischen Methoden
Kovarianz and Korrelation (2/2)
In dieser Korrelationsmatrix sind alle von links oben nach rechts unten diagonal angeordneten Elemente gleich 1. Das liegt daran, dass sie die Varianz für diese Variable in der Kovarianzmatrix enthalten, welche durch die Standardabweichung dieser Zeile und Spalte geteilt wird, d.h. sie wird zweimal durch die Standardabweichung geteilt.
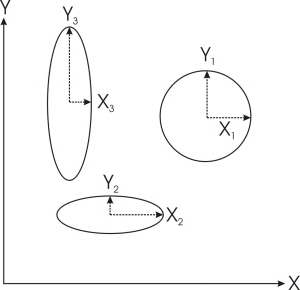
Wenn zwei Variable nicht miteinander korrelieren, dann sind alle Elemente, die sich nicht auf der Diagonalen befinden, gleich Null, sowohl in der Kovarianz- als auch in der Korrelationsmatrix. Die Kovarianzmatrix kann in zwei Dimensionen in Form von Kreisen oder Ellipsen dargestellt werden. Das tun wir, indem im Diagramm die Mittelwerte für eine Klasse und die Standardabweichung beidseits dieses Mittelwertes in Richtung der jeweiligen Achse eingetragen werden. Sind die Daten unkorreliert, erhält man Ellipsen oder Kreise wie in der links gezeigten Grafik. Sind die Standardabweichungen in beiden gezeichneten Dimensionen gleich, entsteht ein Kreis, ansonsten eine Ellipse, deren große Halbachse parallel zu der Achse verläuft, die höhere Werte für die Standardabweichung aufweist.
Liegt eine Kovarianz oder Korrelation vor, dann erhält man Ellipsen, die in einem Winkel zu den beiden Achsen ausgerichtet sind. Dieser Winkel hängt von der Kovarianz zwischen diesen beiden Werten ab. In der Abbildung auf der vorigen Seite ist die Kovarianz für zwei verschiedene Stichproben dargestellt, deren Daten korrelieren. Stichprobe 1 (X1,Y1) besitzt positiv korrelierte Daten, sodass bei einer Erhöhung von x in der Regel auch ein Anstieg von y erfolgt. Stichprobe 3 (X3,Y3) besitzt hingegen negativ korrelierte Daten, sodass eine Zunahme von x in der Regel eine Abnahme von y bedeutet. Die Ausrichtung der Ellipsenachse deutet auf positive oder negative Korrelation hin. Die Korrelation beträgt Null, wenn die große Halbachse der Ellipse entweder mit der x-Achse oder mit der y-Achse übereinstimmt. Die Korrelation erreicht einen maximalen Wert von 1, wenn die große Halbachse in einem Winkel von 45° zu diesen Achsen steht.
Es gibt ein mathematisches Konzept für die Korrelation und Kovarianz, beide lassen sich mit Hilfe der Matrizenrechnung darstellen.
Treten in einem Streudiagramm Strukturen auf, die diagonal zur x-Achse oder y-Achse verlaufen, so hängen die beiden Variablen, zum Beispiel Spektralkanäle bei einem Satellitenbild, miteinander zusammen, sie sind korreliert.