2. Introduction into the Mathematical Methods
Probability (1/2)
Probability, Pr{}, gives us a mechanism whereby we can deal with uncertainty. It is important because it provides a way to analyse the uncertainty associated with an event or a sequence of events.
Probabilities are always assigned a value in the range 0 to 1.
| Pr{} = 0: | there is absolutely no chance that the event will occur |
| Pr{} = 1: | the event will certainly occur |
| Pr{} = 0.5: | there is equal likelihood that the event will or will not occur |

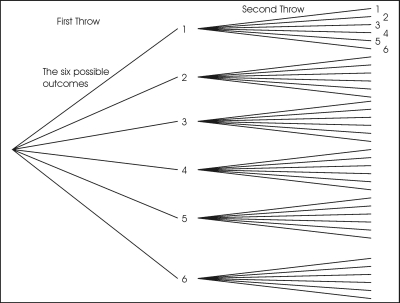
Consider throwing the dice. If the event consists of two throws of the dice, then there are six possible outcomes of the first throw, the first stage of the event and for each of these there are six possible outcomes of the second throw, so that there are 36 possible outcomes in total. Each of these outcomes is equally likely for an unbiased dice and so each combination has a probability of 1/36:
With dice, each number has the same probability that it will be turned up. This does not always apply in life. Consider horse racing, where the probability of six different horses winning two races is given in the table below.
| Horse | Race 1 Probability |
Race 2 Probability |
|---|---|---|
| Raddish | 0.05 | 0.1 |
| Mums the word | 0.25 | 0.22 |
| Pie in the sky | 0.30 | 0.04 |
| Doughboy | 0.06 | 0.35 |
| Atlantis Star | 0.28 | 0.18 |
| Felty | 0.06 | 0.11 |
| Total | 1.00 | 1.00 |
In this table we assume that the two races are independent, where the differences in probabilities are likely to be due to differences in race conditions between the two races, for example run over different distances or differences in the soil conditions. From this table we can see that the probability of Doughboy winning both races is 0.06 · 0.35 = 0.021.
Questions
- What i
has the probability of one sixth when throwing one dice?
- What is the probability of getting 6 as the sum of throwing two dice?