2. Einführung in die mathematischen Methoden
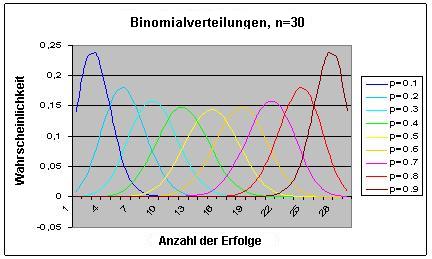
Die Binomialverteilung (1/2)
Die Binomialverteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die sich bei Experimenten oder Aktivitäten verwenden lässt, wenn die folgenden vier Voraussetzungen erfüllt sind:
- Das Ereignis oder Experiment besteht aus einer Folge von n identischen Versuchen, wie beim Werfen eines Würfels.
- Bei jedem Versuch gibt es nur zwei mögliche Ergebnisse, welche üblicherweise als Erfolg und Misserfolg bezeichnet werden. Die Summe der Wahrscheinlichkeiten für Erfolg und Misserfolg muss 1 ergeben.
- Die Wahrscheinlichkeit für einen Erfolg ändert sich nicht von Versuch zu Versuch.
- Die Versuche sind unabhängig.
Ein Beispiel für eine Binomialverteilung könnte das achtmalige Werfen einer Münze sein, mit den Ergebnissen: (K, Z, K, K, K, Z, K, K) (für "Kopf" und "Zahl").
Binomial-Experimente haben für gewöhnlich zum Ziel, die Zahl der Erfolge zu ermitteln, die bei n Versuchen wahrscheinlich ist. Daher könnte man die Frage stellen; "Wie groß ist die Wahrscheinlichkeit für x Erfolge bei n Versuchen?" Bei dieser Art von Experiment ist x eine diskrete Zahl und das Experiment eine diskrete Wahrscheinlichkeitsdichtefunktion.
Geht es um die Frage "Wie groß ist die Wahrscheinlichkeit für 6 mal Kopf bei 8 Münzwürfen?" wenn wir eine Münze achtmal geworfen und das Ergebnis oben erhalten haben, so müssen wir uns zuerst fragen "Kann die Binomialverteilung hier verwendet werden?"
- Sind alle Versuche in der Abfolge identisch? - Ja, bei jedem Versuch handelt es sich um den Wurf einer Münze, oder im Falle eines Würfels um das Werfen eines Würfels.
- Gibt es nur zwei mögliche Ergebnisse? - Ja. Bei einer Münze beträgt die Erfolgswahrscheinlichkeit für jeden Wurf 0,5, weil entweder Kopf oder Zahl herauskommt. Bei einem Würfel gibt es zwar sechs mögliche Ergebnisse, wird jedoch nach der Wahrscheinlichekeit, bei acht Versuchen sechs sechsen zu erhalten gefragt, dann ist die Erfolgswahrscheinlichkeit für jeden einzelnen Versuch eine sechs zu werfen gleich, nämlich 1/6.
- Ist die Wahrscheinlichkeit für einen Erfolg in jedem Versuch gleich groß? - Ja.
- Sind die Versuche unabhängig? - Ja.