Stellen Sie sich zweidimensionale Daten (x,y) vor. Als Minimaldistanzmaß berechnen Sie die Euklidische
Distanz (ED) zwischen den Pixelwerten (xp,yp) und den Mittelwerten
der Klassen, dann weisen Sie jeden Pixel derjenigen Klasse mit der kürzesten Euklidischen Distanz zum
Pixel zu. Sie können alternativ auch die maximale Distanz als Kriterium festsetzen, sodass Pixel, deren Distanz größer ist als der Mittelwert einer Klasse dieser Klasse nicht zugefügt werden.
Zur Euklidischen Distanz:
↓↑
Wir wissen alle, was die Distanz zwischen zwei Punkten bedeutet: Es ist der kürzeste aller möglichen Wege,
um von einem Punkt zu einem anderen Punkt zu kommen.
Die Euklidische Distanz ist in einem euklidischen Vektorraum definiert und stellt die gewöhnliche Bedeutung
der Distanz dar. Wenn Ihnen Vektorräume nichts sagen, denken Sie einfach an diese natürliche Definition
und Sie können diesen Gedanken bis zum Ende des Kapitels im Kopf behalten.
Lassen Sie uns Ihnen für die weiteren Kapitel die folgende Definition geben:
Definition der Distanz in einem euklidischen Raum (das ist ein affiner Vektorraum mit einem gültigen Skalarprodukt,
auch Punktprodukt genannt):
Mit einem Euklidischen Raum ist die Distanz d(P,Q) zwischen zwei Punkten
P und Q der Betrag (die Länge) des Vektors
PQ→:
dP,Q=PQ→
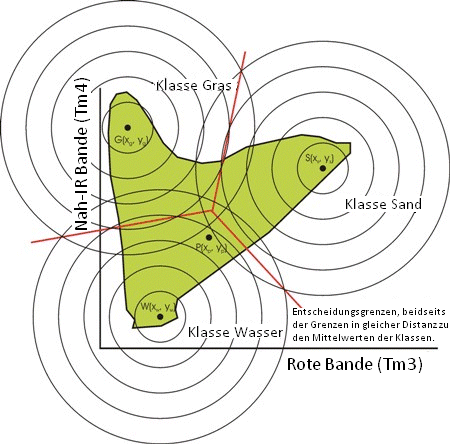
Drei Klassen, ihre Euklidischen Distanzen und ihre minimalen Distanz-Entscheidungsgrenzen
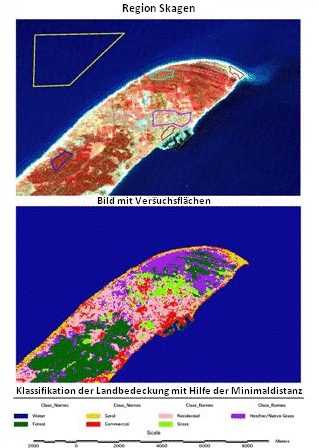
Bild der Region Skagen mit Trainingsflächen (oben) und Klassifizierung nach Minimaldistanz (unten)
Demnach würden wir für drei Klassen drei Distanzen berechnen:
Dann ordnen wir die Pixel der Klasse mit der geringsten Euklidischen Distanz zu, solange die ED kleiner
ist als die festgesetzte Maximaldistanzschwelle.
Die Klassifizierung nach Minimaldistanz nutzt Klassen, die eine Korrelation von Null zueinander aufweisen und
die alle gleiche Varianzwerte besitzen. Es handelt sich daher um einen Sonderfall der Maximum-Likelihood-Klassifizierung,
die wir im nächsten Kapitel kennenlernen.


