4. The Minimum Distance Classifier

Consider for the moment, 2-D data (x,y). With the minimum distance classifier, compute the Euclidean Distance (ED) between the pixel values (xp,yp) and the mean values for the classes, and then allocate the pixel to that class with the shortest Euclidean distance. You can also set a maximum distance criterion, so that pixels further than this distance from a class mean, cannot be assigned to that class.

Background Euclidean Distance: ↓
Zoom Sign
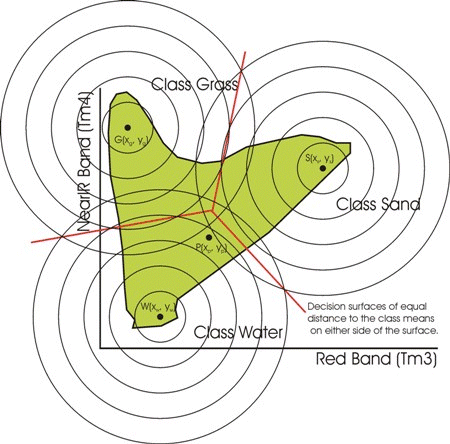
Three classes, their Euclidean Distances and their Minimum Distance Decision Surfaces
Three classes, their Euclidean Distances and their Minimum Distance Decision Surfaces
Zoom Sign
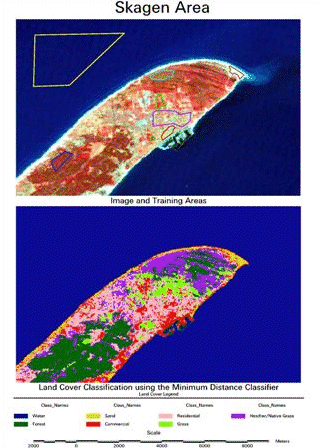
Skagen area
Skagen image, training areas and Minimum Distance Classification

Thus for three classes we would compute three distances:

E D 2  =  ( x p − x g ) 2 + ( y p − y g ) 2 E D 2  =  ( x p − x s ) 2 + ( y p − y s ) 2 E D 2  =  ( x p − x w ) 2 + ( y p − y w ) 2

Then allocate the pixel to the class with the minimum ED, as long as that Euclidean Distance is less than the set maximum distance threshold.

The Minimum Distance Classifier uses classes that you could consider have zero correlation and in which all classes had the same variance values. It is thus a special case of the Maximum Likelihood Classifier that we will meet in the next Chapter.