Supplement 1.7: Radiation quantities and radiometry (2/5)

Spectral quantities

Spectral properties must almost always be taken into account for all radiation quantities. This is done using differential quotients and the indices f for frequency and λ for wavelength. Using radiation power as an example, this is written as follows:

Φ_{f} = \frac{d Φ}{d f}

with

[Φ_{f}] = \frac{W}{Hz}

Φ_{λ} = \frac{d Φ}{d λ}

with

[Φ_{λ}] = \frac{W}{m}

It is often useful to specify power in mW, kW or MW in order to obtain practical numerical values. The same applies to frequencies and wavelengths, which can be specified in kHz, MHz or nm, µm or mm. The following applies when converting quantities related to wavelengths to quantities related to frequencies and vice versa:

Φ_{f} = \frac{λ^{2}}{c} Φ_{λ}

and

Φ_{λ} = \frac{f^{2}}{c} Φ_{f}

The quantity c is the speed of light. The proof can be found on a page about Planck's law of radiation in the question: How do you convert frequencies to wavelengths?

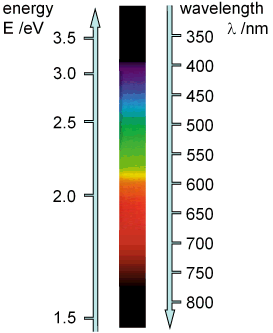
Due to the quadratic expressions in $λ$ and f, the relationship is non-linear. This can be seen, for example, in the spectrum of visible light, which is represented linearly over wavelength but non-linearly over photon energy $E = h f$ .

The spectrum of visible light over the wavelength and the photon energy.

Equations ↓

The radiant energy

Radiant energy corresponds to the temporal integration of radiant power. Conversely, radiant power is equal to the temporal derivative of radiant energy:

Q = \int Φ d t

Φ = \frac{d Q}{d t}

Formula symbol: $Q$
Unit of measurement: Joule, $[Q] = J$

This parameter is important, for example, for photosynthesis in vegetation, or for the yield of photovoltaics in regions with varying amounts of sunshine.

The symbol Q is borrowed from thermodynamics, where it denotes a quantity of heat. The symbol E, commonly used in mechanics for kinetic energy, is not appropriate for radiant energy, as E is often used in radiometry to denote irradiance. In quantum physics, E denotes photon energy. Supplement 1.6 on radiation pressure refers to both photon energy and irradiance; to distinguish between the two, SEOS uses the symbol $E_{r a d}$ for irradiance.