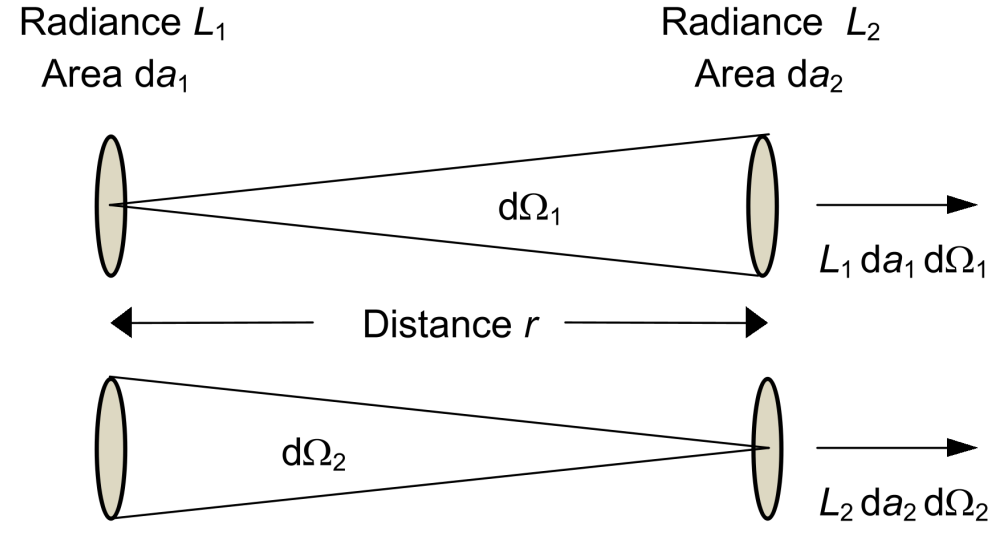Supplement 1.7: Radiation quantities and radiometry      (6/9)

The radiance

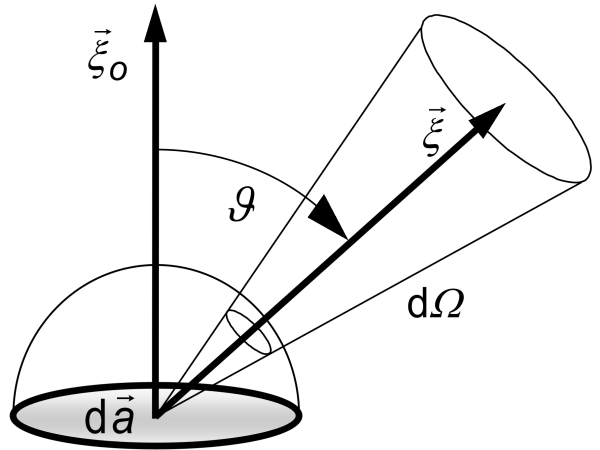
The radiance L is the most fundamental radiometric quantity. It combines all of the dependencies mentioned so far: radiant power ϕ, the radiating (or irradiated) area a, a direction in space and the solid angle Ω around this direction.

The radiance characterises the radiant power emitted by the area into this solid angle:

Formula symbol: $L$
Unit of measurement: Watts per square metre per steradian, $\left[L\right]=\frac{\text{W}}{{\text{m}}^2\cdot \text{sr}}$

The radiance of a surface da in a solid angle dΩ around the direction $\overrightarrow{\xi }$. Viewed from this direction, the surface da appears reduced by cosϑ. ${\overrightarrow{\xi }}_o$ is the normal vector on da.

The special feature of radiance is that it is a characteristic property of the radiation source. Its value remains unchanged as the radiation propagates through space, provided that no changes occur due to absorption or scattering. As the distance from the source increases, the solid angle Ω encompasses a quadratically increasing area. On the other hand, this is compensated by the quadratically decreasing irradiance on the surface, which is why the radiance remains constant. This is clearly illustrated in the following graphic.

Two opposing surfaces da₁ and da₂. The left surface emits radiation with a radiance of L₁, while the right surface receives radiation with a radiance of L₂.

The situation from the perspective of the emitting surface da₁ is shown above, and the situation from the perspective of the irradiated surface da₂ is shown below. Obviously, the following applies:

Substituting into the relationships given in the graph yields $L_1=L_2$.