Supplement 1.8: Lambert emitters, cosine emitters      (3/4)

Further examples      ...Continued from previous page

White walls, white glass panes      ...continued

Now, one could argue that the distance to the viewed surface has remained the same. Therefore, we will now examine the situation with a constant vertical distance to the frosted glass.

The observer now observes in a plane parallel to the frosted glass. Under the observation angle ϑ, the distance from R increases to the value R'. The solid angle Ω should remain the same.

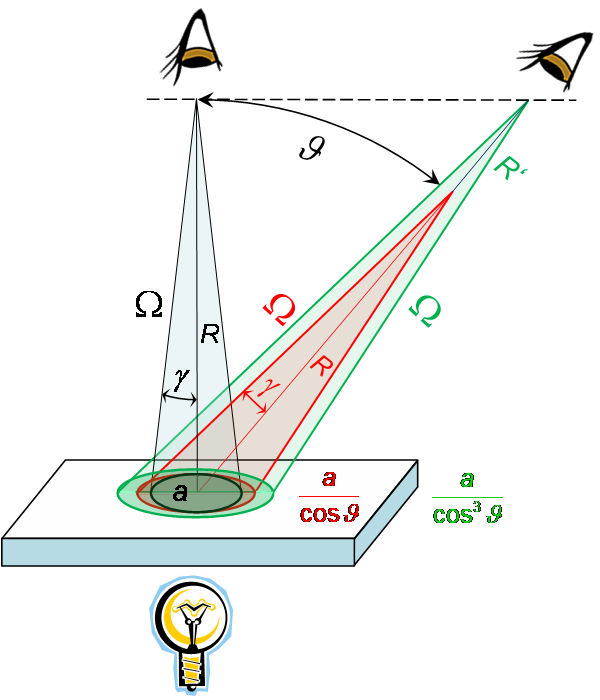
For the view at angle ϑ at the previous distance R, the result from the previous page (red) applies:

In a right-angled triangle, the following applies to the distance R':

This will result in (green):      $\Omega =a/\left(R{\text{'}}^2{cos}^3\vartheta \right)$

The area under consideration has thus grown by a factor of a/cos³ϑ compared to the vertical orientation.

On the other hand, it can be written that:

The factor $R{\text{'}}^2/R^2$ compensates for the decrease in irradiance (W/m²) expected according to the photometric distance law with the square of the distance from the light source. This must be the case, otherwise the radiant intensity would not be maintained..