Supplement 1.8: Lambert-straler, cosinusstraler      (3/4)

 

Meer voorbeelden      ...Vervolg van de vorige pagina

Witte muren, witte ruiten      ...vervolg

Nu kan men tegenwerpen dat de afstand tot het geziene oppervlak gelijk is gebleven. Daarom onderzoeken we nu de situatie bij een gelijkblijvende verticale afstand tot het matglas.

Zoom Sign
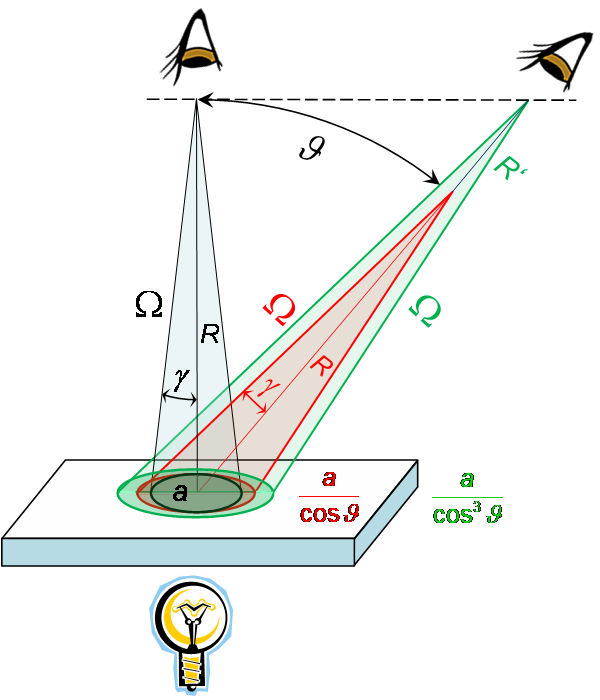
Matglazen ruit bekeken vanuit verschillende hoeken
De waarnemer kijkt nu in een vlak parallel aan de matte schijf. Onder de waarnemingshoek ϑ vergroot de afstand van R tot de waarde R'. De ruimtehoek Ω moet gelijk blijven.
Vergelijkingen ↓

Voor het zicht onder de hoek ϑ op de huidige afstand R geldt volgens het resultaat van de vorige pagina (rood):

Ω=a/ ( R 2 cosϑ )

In een rechthoekige driehoek geldt voor de afstand R':

cosϑ=R/ R'

Hierdoor wordt (groen):      Ω=a/ ( R ' 2 cos 3 ϑ )

Het bekeken oppervlak is dus ten opzichte van de verticale oriëntatie met een factor a/cos³ϑ gegroeid.

Anderzijds kan worden geschreven:

a/ cos 3 ϑ = R ' 2 R 2 ⋅ a cosϑ

De factor R ' 2 / R 2 compenseert precies de volgens de fotometrische afstandswet te verwachten afname van de s tralingsintensiteit (W/m²) met het kwadraat van de afstand tot de lichtbron. Dit moet zo zijn, anders zou de stralingsintensiteit niet behouden blijven.

De stralingssterkte die met het oog onder een vaste ruimtehoek wordt waargenomen, blijft dus ook bij een variabele afstand tot het lichtgevende oppervlak behouden.