Ergänzung 1.8: Lambert-Strahler, Kosinus-Strahler      (4/4)

Weitere Beispiele      ...Fortsetzung von der vorherigen Seite

Kugelleuchten

Kugelförmige Leuchten aus Mattglas oder mattiertem Kunststoff, die man oft zu Hause und auch im Freien nutzt, können gute Lambert-Strahler sein. Im Beispiel auf der vorherigen Seite haben wir gesehen, dass die Strahlstärke von Mattglas nicht von der Neigung des Glases abhängt. Dies gilt daher auch für gekrümmte oder eben kugelförmige Glasoberflächen.

Im Foto links ist diese Eigenschaft recht gut realisiert: die Leuchte erscheint über ihre ganze Fläche unabhängig von der Neigung fast gleich hell. Da die Strahl­stärke der Leuchte - abgesehen von Abweichungen, die durch die mecha­nische Halterung zustande kommen - in alle Raumrichtungen gleich groß ist, liegt hier ein isotroper Strahler vor.

Bei der Leuchte im rechten Bild ist dies nicht der Fall. Vielmehr sieht man einen zentralen sehr hellen Bereich. Die äußeren Flächen sind deutlich dunkler. Die Leuchte ist daher kein Lambert- oder Kosinus-Strahler.

Leuchten mit flachem oder nur gering gewölbtem Mattglas können ebenfalls beide Eigenschaften zeigen. Dies gilt auch für die in den Leuchten einge­setzten Lampen, die oft mit einem mattierten Glas- oder Kunst­stoffgehäuse erhältlich sind.

Die Verdunkelung des Sonnenrands

Randverdunkelung der Sonne. Links unten ist ein großer Sonnenfleck zu sehen.
Quelle: NASA Marshall Space Flight Center, USA

Nun könnte man fragen, ob die Sonne eine eher gute oder eher schlechte Kosinus-Kugelleuchte ist? Mittelt man über die turbu­lenten Strukturen der leuchtenden Photo­sphäre hinweg, so ergibt sich das rechts gezeigte Bild, in dem eine deutliche Ver­dunkelung von der Mitte hin zum Rand beobachtet wird.

Verursacht wird die Randverdunkelung durch die Absorption und Streuung der Strahlung der Photo­sphäre in den höheren kälteren Schichten der Sonnenatmosphäre. Diese Verluste hängen von der Wellenlänge ab, der Effekt ist im UV und Blau deutlich höher als im Rot und IR.

Ein Modell der Randverdunkelung wurde von Jeremy Tatum in dem Lehrbuch Stellar Atmospheres vorgestellt, das die Strahlstärke $I$ als Funktion des Abstands r von der Mitte der Sonnenscheibe beschreibt:

Der Parameter u ist der Randverdunkelungskoeffizient, mit Werten von 0,56 bei 600 nm (orange) und 0,95 bei 320 nm (UV). a ist der Radius der Sonnenscheibe. Setzt man a=1 und normiert den Mittenabstand r auf den Maximalwert 1, ergeben sich die folgenden Kurven.

Lösungen der oben gezeigten Gleichung mit (von unten nach oben) u=1,0 - 0,8 - 0,6 - 0,4 - 0,2 - 0,0. Für u=1,0 ergibt sich ein Halbkreis, für u=0,0 ist es die obere Randlinie der Grafik.
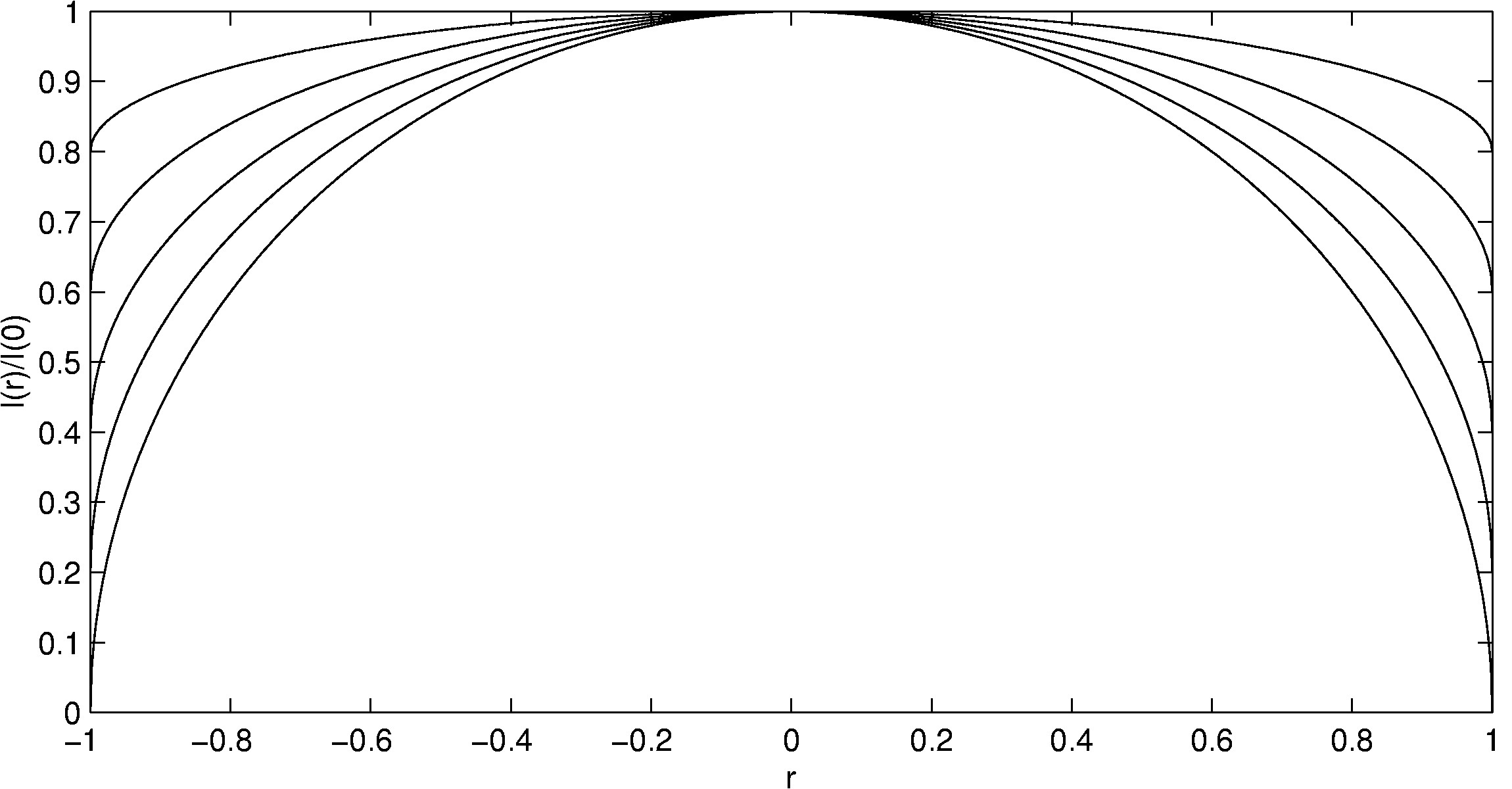
Quelle: Jeremy Tatum: Stellar Atmospheres, Kapitel 6.