Supplement 1.8: Lambert-straler, cosinusstraler      (4/4)

Meer voorbeelden      ...Vervolg van de vorige pagina

Kogelvormige lampen

Bolvormige lampen van matglas of ge­matteerd kunststof, die vaak thuis en ook buiten worden gebruikt, kunnen goede Lambert-stralers zijn. In het voorbeeld op de vorige pagina hebben we gezien dat de stralingssterkte van matglas niet afhankelijk is van de helling van het glas. Dit geldt dus ook voor gebogen of bolvormige glasopper­vlakken.

Op de foto links is deze eigenschap goed te zien: de lamp lijkt over het hele oppervlak bijna even helder, ongeacht de hellingshoek. Omdat de stralingssterkte van de lamp - afgezien van afwijkingen die door de mechanische bevestiging ontstaan - in alle richtingen gelijk is, is er hier sprake van een isotrope straler.

Bij de lamp op de rechterfoto is dit niet het geval. In plaats daarvan ziet men een centraal, zeer helder gebied. De buitenste oppervlakken zijn duidelijk donkerder. De lamp is daarom geen Lambert- of cosinus-straler.

Lampen met vlak of slechts licht gewelfd matglas kunnen ook beide eigen­schappen vertonen. Dit geldt ook voor de lampen die in de lampen worden gebruikt, die vaak verkrijgbaar zijn met een matte glazen of kunststof behuizing.

De verduistering van de rand van de zon

Randverduistering van de zon. Linksonder is een grote zonne­vlek te zien.
Bron: NASA Marshall Space Flight Center, USA

Nu zou men zich kunnen afvragen of de zon een eerder goede of eerder slechte cosinusbolvormige lichtbron is? Als men het gemiddelde neemt van de turbulente structuren van de lichtgevende fotosfeer, krijgt men het rechts afgebeelde beeld, waarin een duidelijke verduistering van het midden naar de rand toe waarneembaar is.

De verduistering aan de rand wordt veroor­zaakt door de absorptie en verstrooiing van de straling van de fotosfeer in de hogere, koudere lagen van de zonneatmosfeer. Deze verliezen zijn afhankelijk van de golflengte; het effect is in het UV- en blauwe spectrum duidelijk groter dan in het rode en IR-spectrum.

Een model van randverduistering werd door Jeremy Tatum voorgesteld in het leerboek Stellar Atmospheres, waarin de stralingssterkte $I$ wordt beschre­ven als functie van de afstand r tot het midden van de zonneschijf:

De parameter u is de randverduisteringscoëfficiënt, met waarden van 0,56 bij 600 nm (oranje) en 0,95 bij 320 nm (UV). a is de straal van de zonneschijf. Als we a=1 instellen en de middenafstand r normaliseren tot de maximale waarde 1, krijgen we de volgende curven.

Oplossingen van de hierboven weergegeven vergelijking met (van onder naar boven) u=1,0 - 0,8 - 0,6 - 0,4 - 0,2 - 0,0. Voor u=1,0 resulteert dit in een halve cirkel, voor u=0,0 is dit de bovenste randlijn van de grafiek.
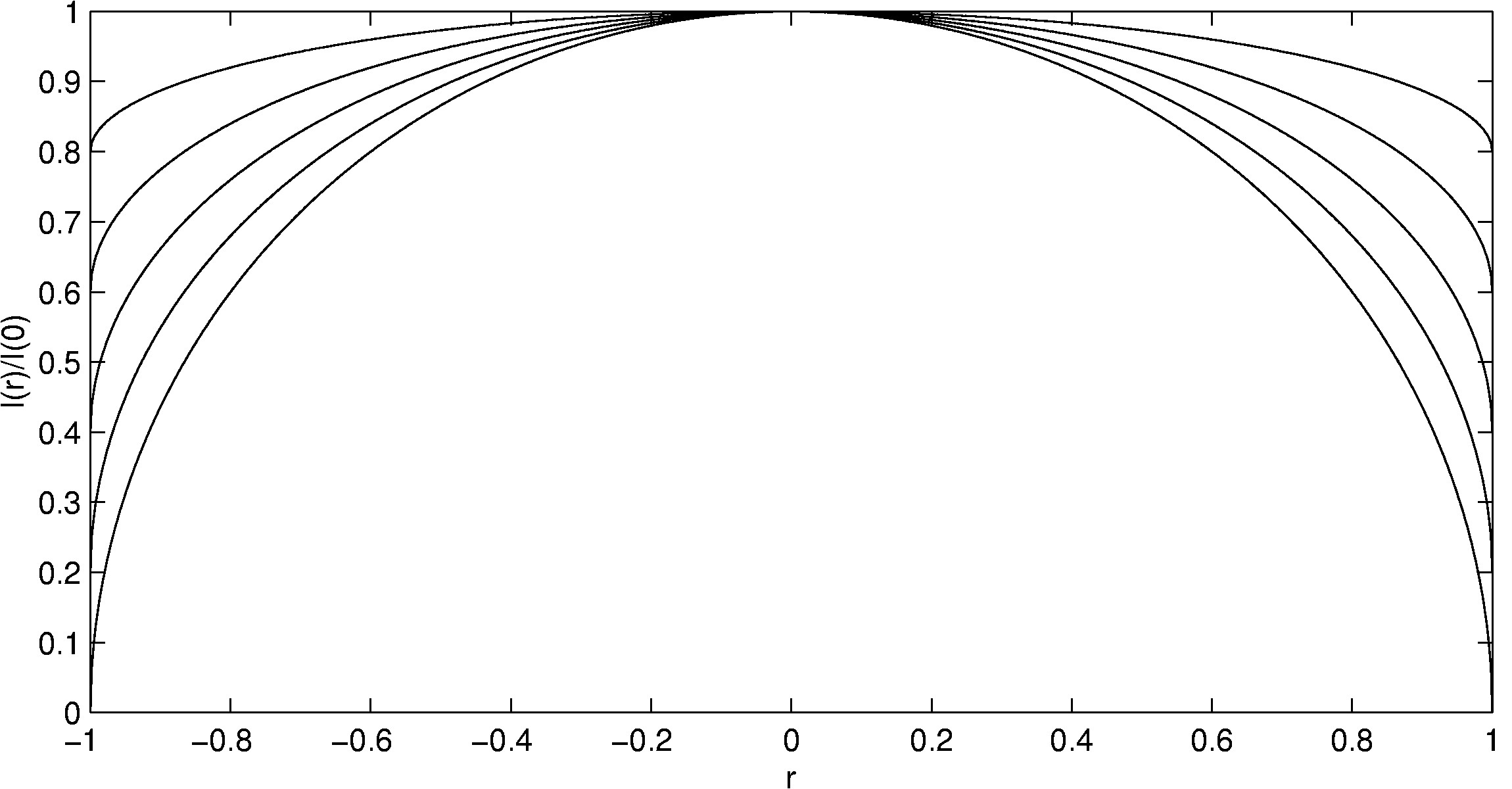
Bron: Jeremy Tatum: Stellar Atmospheres, hoofdstuk 6.