2. Thermal radiation

The colour: Wien's displacement law

In the same way as for the area under the Planck spectra of black bodies, we are now interested in the wavelength of the greatest brightness. This maximum is apparently only dependent on temperature, with a tendency towards smaller wavelengths with increasing temperature. In the frequency representation, there is a tendency towards larger frequencies with increasing temperature. According to which functional dependence does this happen?

We start out from the frequency representation of the spectral energy density as we did for discussing the Stefan-Boltzmann law.

u f = dU df = 8πh c 3 f 3 exp{ hf / kT }−1

The search for the maximum of the radiation law is an extremum problem of mathematical analysis: deriving and zeroing the derivative. This is somewhat difficult because it is a transcendental equation: fmax is found in first power and simultaneously as the exponent of the e-function. The detailed calculation can be found in the Supplement 2.4.

The result is:

f max T =5.879⋅ 10 10 1/ (s·K)

The frequency of the radiation maximum of a black body increases proportionally with its temperature.

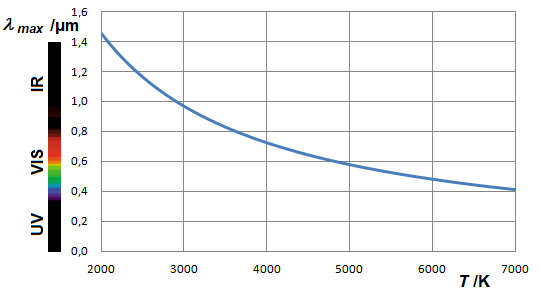
The position of the maximum as a function of the wavelength results from an analogous calculation, see Supplement 2.4. The result is:

λ max T=2.90⋅ 10 −3 m·K

In this case, we find an inverse proportionality: the maxima of the Planck graph as a function of wavelength follow a hyperbola.

This is called Wien's displacement law.

The maxima of Planck's radiation law change their spectral location in a remarkably clear manner: the wavelength of the maximum multiplied with the absolute temperature is a constant. Or: the ratio of the frequency of the maximum and the absolute temperature is a constant.
Equations ↓
Maximum at 2000 - 7000 K Maximum at 100 - 2000 K
Maximum at 2000 - 7000 K
Wavelength in µm of the radiation maximum for black bodies. Left: At temperatures between 2000 and 7000 K. The radiating solar surface has a temperature of about 5800 K. Right: At temperatures between 100 and 2000 K. 300 K corresponds approximately to room temperature.
Source: Rainer Reuter, University of Oldenburg, Germany.

Knowing one value pair, the wavelength of the frequency of the maximum can be calculated for every other temperature through the rule of three. It is thus not necessary to memorise the value on the right of Wien's displacement law. It is sufficient, to know that:

λ max ⋅T=const.
Task: Maxima of the Planck graph of several radiators ↓