Supplement 4.4: Polarisatie van elektromagnetische golven: Jones vectoren en Jones matrices (2/2)

Optische interacties als 2×2 matrix: Jones matrices

Na een optische interactie markeren we de veldcomponenten als gestippelde grootheden. Ze zijn een lineaire combinatie van de primaire componenten:

Geschreven als een matrix:

De amplitude-transformatiematrix $A$ is de Jones matrix.

Het doel is om een Jones matrix te vinden voor elk type optische componenten die de polarisatie van licht veranderen. Het optische effect van die componenten hangt af van hun oriëntatie ten opzichte van de lichtbundel: Een lineaire polarisator bijvoorbeeld beïnvloedt gepolariseerd licht afhankelijk van zijn oriëntatie op totaal verschillende manieren. Dit geldt in dezelfde mate voor de splitsing van lichtstralen bij het raken van een brekend oppervlak (glas, water...).

Dit kan worden gevonden door een enkele Jones matrix te formuleren voor een bepaalde oriëntatie van alle componenten of optische interacties die de polarisatie beïnvloeden. De matrix voor andere oriëntaties kan worden opgesteld door het gepolariseerde licht aan te passen door de y en z-coördinaten te roteren naar de positie waarin het moet interageren met de component en het vervolgens terug te brengen naar de beginpositie.

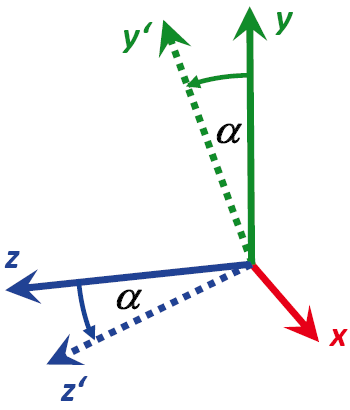
Een rotatie van de y- en z-coördinaten met een hoek $\alpha$ in een ander y'- en z'-coördinatensysteem zoals weergegeven in de volgende grafiek ...

... wordt als volgt berekend:

De coëfficiënten van het stelsel vergelijkingen zijn de elementen van de rotatiematrix:

Als we de amplitude-transformatiematrices van componenten met een bepaalde oriëntatie $A$ noemen en dezelfde componenten onder een hoek $\alpha$ met $A(\alpha )$, dan wordt het:

Voorbeelden van Jones matrices staan in de volgende tabel. Ze gelden voor ideale eigenschappen, dat wil zeggen absorptie- en reflectievrije componenten en perfect vlakke oppervlakken.

Jones matrix	Onderdeel of interactie
$\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right)$	Lineaire polarisator die langs de y-as uitzendt
$\left(\begin{array}{cc}{\text{e}}^{-i\phi /2}& 0\\ 0& {\text{e}}^{i\phi /2}\end{array}\right)$	Vertrager met faseverschil $\phi$ van de golfdelen, snelle as in y-richting
$\left(\begin{array}{cc}{\text{e}}^{-i\pi /4}& 0\\ 0& {\text{e}}^{i\pi /4}\end{array}\right)$	$\lambda /4$ vertrager ($\lambda /4$ golfplaat) met $\phi =\pi /2$, snelle as in y-richting
$\left(\begin{array}{cc}{\text{e}}^{-i\pi /2}& 0\\ 0& {\text{e}}^{i\pi /2}\end{array}\right)$	$\lambda /2$ vertrager ($\lambda /2$ golfplaat) met $\phi =\pi$, snelle as in y-richting
$met\left(\begin{array}{cc}{t}_{\parallel }& 0\\ 0& t_{\perp }\end{array}\right)$	Fresnelbreking bij een diëlektrisch materiaal met een invalshoek ${\delta }_i$ en een brekingshoek ${\delta }_t$, waarbij de y-as in het invalsvlak ligt en de z-as loodrecht op het invalsvlak staat, en met de Fresnel-amplitudecoëfficiënten voor breking: $\begin{array}{l}{t}_{\parallel }=2sin{\delta }_{t}cos{\delta }_i/\left(sin({\delta }_i+{\delta }_t)cos({\delta }_i-{\delta }_t)\right)\\ t_{\perp }=2sin{\delta }_{t}cos{\delta }_i/sin({\delta }_i+{\delta }_t)\end{array}$
$\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\cdot \left(\begin{array}{cc}{r}_{\parallel }& 0\\ 0& r_{\perp }\end{array}\right)$	Fresnel reflectie op een diëlektrisch materiaal met een invalshoek ${\delta }_i$ en brekingshoek ${\delta }_t$, de y-as ligt in het invalsvlak en de z-as staat loodrecht op het invalsvlak, en met de Fresnel amplitudecoëfficiënten voor reflectie: $\begin{array}{l}{r}_{\parallel }=-tan\left({\delta }_i-{\delta }_t\right)/tan\left({\delta }_i+{\delta }_t\right)\\ r_{\perp }=-sin\left({\delta }_i-{\delta }_t\right)/sin\left({\delta }_i+{\delta }_t\right)\end{array}$ De linkermatrix is het resultaat van de richtingsverandering van de lichtpropagatie door reflectie.
$\left(\begin{array}{cc}cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{array}\right)$	Rotatie door de hoek $\alpha$

Het effect van meerdere componenten op een rij wordt berekend uit het product van de respectieve matrices. Voor n componenten:

waarbij $A_1$ de eerste en $A_n$ de laatste verzonden component in een rij is. De matrices zijn niet commutatief (de componenten omkeren zou ook gevolgen hebben).