Ergänzung 7.1: Die hydrographische Lidar-Gleichung (1/3)

Darstellung der Gleichung

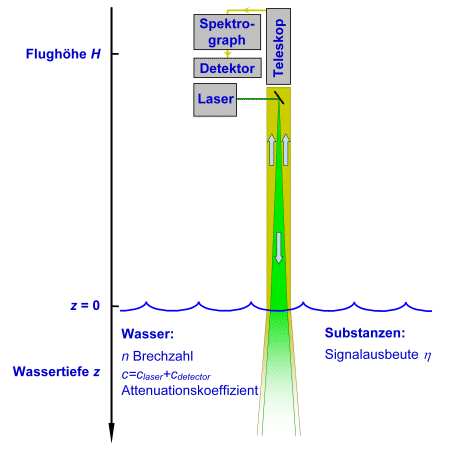
Wir betrachten ein Lidar, das in einem Flugzeug (oder einem anderen Fluggerät) in der Flughöhe H über einem Gewässer eingesetzt wird.

Elemente eines hydrographischen Lidar in einem Flugzeug über einem Gewässer.

Der Laser sendet Lichtpulse mit der Wellenlänge λ_laser zur Wasseroberfläche. Die Vertikalkoordinate ist mit z bezeichnet; an der Wasseroberfläche ist z=0, und z ist positiv nach unten.

In der Wassersäule wird das Laserlicht nach dem Lambertschen Extinktionsgesetz durch Lichtabsorption und -streuung geschwächt. In einer vorgegebenen Tiefe z findet sich daher nur noch der Bruchteil exp(-c_laserz) des an der Wasseroberfläche vorhandenen Laserlichts. Die Größe c_laser ist der Attenuationskoeffizient des Lichts bei der Laserwellenlänge. Ist die Verteilung absorbierender und streuender Substanzen tiefenabhängig, so wird der Attenuationskoeffizient ebenfalls tiefenabhängig, und in der Tiefe z ist der Bruchteil

exp (- \int_{z' = 0}^{z} c_{l a s e r} (z') d z')

des Laserlichts vorhanden (z' ist die Integrationsvariable, z die betrachtete Tiefe).

Ein in der Tiefe z erzeugtes Signal (Fluoreszenz, Streuung) wird auf dem Weg zur Wasseroberfläche ebenfalls durch Absorption und Streuung geschwächt. Registriert der Detektor das Signal bei einer (durch den Spektrographen so vorgegebenen) Wellenlänge λ_detector, so wird dies mit dem Attenuationskoeffizienten c_detector beschrieben. Für die Lichtschwächung von der Oberfläche bis zur Tiefe z und zurück zur Oberfläche gilt somit:

exp (- \int_{z' = 0}^{z} (c_{l a s e r} (z') + c_{det e c t o r} (z')) d z')

Zur Vereinfachung werden die Attenuationskoeffizienten im Weiteren zu einer Größe c=c_laser+c_detector zusammengefasst. Die Lichtausbreitung in der Atmosphäre wird als verlustfrei angenommen.

Substanzen in der Wassersäule werden mit einer Signalausbeute η beschrieben, die durch molekulare optische Eigenschaften (z.B. die spezifische Fluoreszenzausbeute) und die Konzentration zustande kommt. Die von dem Detektor des Lidar gemessene optische Leistung aus einem infinitesimalen Tiefenintervall dz in der Tiefe z ist dann:

d P \propto η \frac{exp (- \int_{z' = 0}^{z} c (z') d z')}{{(z + n H)}^{2}} d z

Die Größe (z+nH)² kommt durch das photometrische Entfernungsgesetz zustande: die Helligkeit einer Lichtquelle nimmt mit dem Quadrat der Entfernung ab. Die Brechzahl n des Wassers berücksichtigt die Lichtbrechung an der Wasseroberfläche. Der Einfluss von Wellen auf den Strahlengang wird hier nicht betrachtet.

Dies ist die hydrographische Lidar-Gleichung. Spezielle instrumentelle Eigenschaften des Lidar wie zum Beispiel die Leistung des Lasers, die Lichtstärke des Teleskops etc., werden hier nicht betrachtet, weshalb die Beziehung als Proportionalität formuliert ist.

Lösung der Gleichung

Ein Lidar-Signal aus einer endlich tiefen Wasserschicht zwischen z₁ und z₂ folgt durch Integration:

P_{z_{1} \to z_{2}} \propto exp (- \int_{0}^{z_{1}} c d z) \cdot \int_{z_{1}}^{z_{2}} η \frac{exp (- \int_{z_{1}}^{z} c d z')}{{(z + n H)}^{2}} d z

Das zweite Integral wird mit $Φ$ bezeichnet:

Φ = \int_{z_{1}}^{z_{2}} η \frac{exp (- \int_{z_{1}}^{z} c d z')}{{(z + n H)}^{2}} d z

Setzt man w=(z+nH)/nH und nimmt an, dass c und η zwischen z₁ und z₂ konstant sind, kann man das Integral als

Φ = η \frac{exp (n H c w_{1})}{n H} \int_{w_{1}}^{w_{2}} \frac{exp - (n H c w)}{w^{2}} d w

schreiben. Mit der Substitution

d w = - \frac{1}{n H c + \frac{2}{w}} \frac{w^{2}}{exp - (n H c w)} d \frac{exp - (n H c w)}{w^{2}}

und nähert man nHc»2/w, was c»2/(z+nH) entspricht und allgemein zutreffen wird, wird die Integration:

Φ = \frac{η}{c} \frac{1}{{(n H)}^{2}} (\frac{1}{w_{1}^{2}} - \frac{exp - (n H c (w_{2} - w_{1}))}{w_{2}^{2}})

Das Lidar-Signal aus der Wasserschicht zwischen z₁ und z₂ wird damit:

P_{z_{1} \to z_{2}} \propto exp (- \int_{0}^{z_{1}} c d z) \cdot \frac{η}{c} (\frac{1}{{(z_{1} + n H)}^{2}} - \frac{exp - (c (z_{2} - z_{1}))}{{(z_{2} + n H)}^{2}})

Diese Beziehung ist ganz allgemein anwendbar, um die Signale von Schichtungen in der Wassersäule zu analysieren. Der Zusammenhang zwischen der mit einem Lidar gemessenen Zeitfunktion $P (t)$ der Signalleistung und der hier angegebenen Tiefenfunktion $P (z)$ ist durch die Gleichung

z = c t / 2

gegeben, welche die Laufzeit t des Lichts mit der zurückgelegten Entfernung z verknüpft; der Faktor 2 im Nenner entsteht durch das zweimalige Durchlaufen (hin und zurück) der Strecke z. Dies setzt allerdings voraus, dass die Pulsdauer $Δ t$ der Laserpulse hinreichend kurz ist, zumindest kürzer als die Dicke der noch zu erfassenden Schichten:

Δ t \leq \frac{2}{c} (z_{2} - z_{1})

Da das Licht in Wasser in einer Nanosekunde eine Strecke von etwa 20 cm zurücklegt, entspricht 1 ns Pulsdauer eines Lasers einer Tiefenauflösung von 10 cm; Schichtungen mit dieser Dicke bilden sich im gemessenen Signal gerade noch ab.

Längere Pulsdauern ’verschmieren‘ dünnere Schichtungsstrukturen. Mathematisch wird dies durch eine sogenannte Faltung der zeitlichen Systemfunktion des Lidar mit dem Signal, das mit einem unendlich kurzen Laserpuls erhalten wird, beschrieben; die Entfaltung des gemessenen Signals erlaubt dann, letzteres zu berechnen. Dies ist in der weiterführenden Literatur dargestellt.

Auf der folgenden Seite betrachten wir einige Sonderfälle, die sich aus der zeitlichen Integration des gemessenen Signals über seine gesamte Zeitdauer am Detektor ergeben. Durch die zeitliche Integration geht die Information über Schichtungen der Wassersäule verloren. Man erhält dann Summenparameter wie beispielsweise den mittleren Attenuationskoeffizienten in den oberflächennahen Wasserschichten. Laserfluorosensoren messen zeitlich integrierend, im Gegensatz zum zeitauflösend messenden Lidar.

Fernerkundung mit Lasern

Ergänzung 7.1: Die hydrographische Lidar-Gleichung (1/3)

Darstellung der Gleichung

Lösung der Gleichung