Supplement 7.3: Raman Scattering (4/6)
Quantum theory
Macroscopic masses that are bonded together by springs can vibrate - within certain limits - with any given (continuously distributed) amplitudes and corresponding energy levels. Nuclear or atomic masses behave differently: the vibrational energy levels are rather discrete (quantised) and the energy differences of allowed vibrational states are constant. This is discussed on page 2 of the supplement on fluorescence.
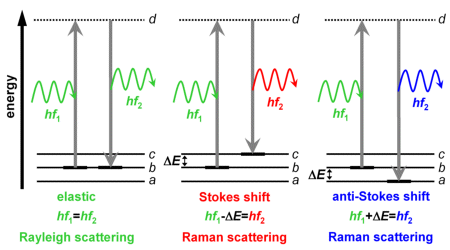
Shown on the right are three vibrational states (a, b, c). They differ from one another with respect to their energy by ΔE. It is assumed that the molecule is in the middle energy state b.
In quantum theory, light is considered as made up of particles called photons. Read more on electromagnetic waves and photons in the SEOS tutorial Understanding Spectra from the Earth. A photon may be absorbed by a molecule if it has the required photon energy to bring the molecule into a higher electronic state. This topic is also further explained in the supplement on fluorescence.
But if the photon energy is too low for the molecule to attain a higher energy state, the molecule transits into a very short-lived state (d) from which it then transits very quickly - within a matter of femtoseconds (1 fs=10-15 s) - into a lower state. The energy state (d) is only temporary and is therefore referred to as a virtual state. On the diagram, it is shown as a dotted line.
More crucial now is to consider which lower energy state does the electron take on from (d)?
- If it takes on the same state which it had before excitation (b on the diagram), a photon having the same energy is emitted. Its direction is different from that of the absorbed photon. Because the photon's direction changes, this process is referred to as light scattering, or Rayleigh scattering, to be exact. The photon energy remains unchanged, so it is an elastic scattering.
- If it takes on a state having a higher vibrational energy (c on the diagram), a photon having an energy level lowered by ΔE is emitted. ΔE remains in the molecule as vibrational energy. This type of scattering is inelastic and corresponds to the Stokes shift Raman scattering.
- If it takes on a state having a lower vibration energy level (a on the diagram), a photon having an energy level that is increased by ΔE is emitted. The vibrational energy of the molecule is reduced by ΔE. This type of scattering is likewise inelastic and corresponds to anti Stokes shift Raman scattering.
According to the electromagnetic wave model, Stokes shift and anti Stokes shift Raman scattering should exhibit the same intensity. The photon model, however, explains why this is not so. The population number of the vibrational states (a), (b) and (c) follow the Boltzmann-distribution explained in Chapter 2, which says that lower energy states have higher population numbers than higher states. Hence, the majority of molecules are actually found in state (a) and are not capable of reaching a lower state after photon absorption; only molecules having the (b) or (c) states can do this.
The equations indicated in the diagram above are based on the photon energy E=hf (with the Planck constant h and the frequency f of the corresponding electromagentic wave) and the energy difference ΔE of the molecular vibrational states. These equations denote the energy balance of the scattering processes in a clear and simple manner.
Numerical values for energies can be expressed in Joule (J), wattseconds (Ws) or electron volts (eV) (also explained in the SEOS tutorial Earth Spectra). In spectroscopy, wave numbers expressed in units of cm-1 are preferred. Apart from physical constants this corresponds to the energy:
Numerical values of wavenumbers are therefore computed by using the reciprocal value of the wavelength λ given in centimetres.
