14. Lösung der Übungsaufgaben in Kapitel 8
3. Das Teleskop
- Gesichtsfeld eines Detektors mit Blende
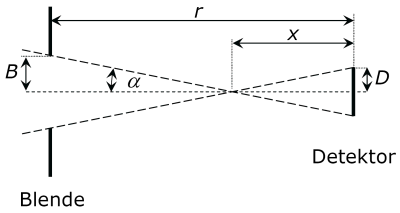
Die einfachste Möglichkeit, das Gesichtsfeld eines Detektors zu begrenzen, besteht in der Verwendung einer Blende.
Ein Detektor mit Blende zur Begrenzung des Gesichtsfelds.Detektor und Blende sind im Abstand r angeordnet. Der Radius des Detektors ist D, der Radius der Blende ist B. α ist der größtmögliche halbe Gesichtsfeldwinkel.
Aufgabe
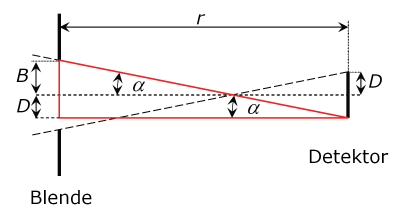
Bestimmen Sie bitte aus den geometrischen Verhältnissen eine Gleichung für den Gesichtsfeldwinkel α in Abhängigkeit von B und D.Hinweis: Finden Sie ein rechtwinkliges Dreieck, das den Winkel α sowie die Radien B und D enthält.
Lösung:
Geometrie des Detektors mit Blende zur Begrenzung des Gesichtsfelds. -
Gesichtsfeld eines Detektors mit Linse und Blende
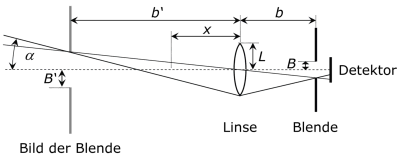
Die Lichtausbeute eines Detektors mit Blende ist sehr gering. Viel bessere Lichtausbeuten erhält man, wenn die Anordnung mit einer Linse ergänzt wird.
Ein Detektor mit Sammellinse und Blende zur Begrenzung des Gesichtsfelds.Der maximale Empfangswinkel α wird durch die Linse (mit Radius L und Brennweite f) und die Blende im Abstand b festgelegt. Die empfindliche Fläche des Detektors hinter der Blende sei so groß gewählt, dass sie den Strahlengang nicht begrenzt. Der größtmögliche halbe Gesichtsfeldwinkel α ergibt sich aus dem Bild der Blende B' im Abstand b' von der Linse.
Aufgabe
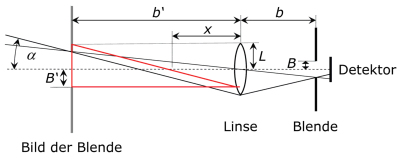
a) Bestimmen Sie bitte aus den geometrischen Verhältnissen und mit den Abbildungsgleichungen für eine Linse eine Beziehung für den Gesichtsfeldwinkel α in Abhängigkeit von L, B, b und f.
b) Wie vereinfacht sich das Ergebnis für b=f, d.h. wenn die Blende im Abstand der Brennweite der Linse steht?Hinweis: Finden Sie wieder ein rechtwinkliges Dreieck, das nun den Winkel α sowie die Größen L, B' und b' enthält. Nutzen Sie die Linsenabbildungsgleichungen, um aus B' und b' die Beziehung als Funktion von B und b darzustellen.
Lösung:
Geometrie des Detektors mit Sammellinse und Blende zur Begrenzung des Gesichtsfelds.a)
b)
