Flugzeuggestützte Meeresüberwachung 4:
Interferenz von Öl auf dem Wasser: Ergänzung
Szenario
|
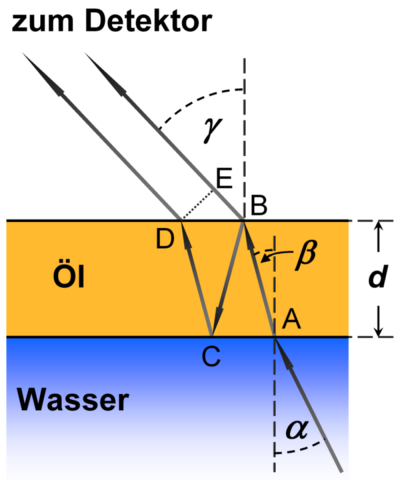
Wir wollen genauer verstehen, wie die Interferenzstreifen zustande kommen, die man mit dem Mikrowellenradiometer beobachten kann.
In der Abbildung ist der geometrische Wegunterschied Δs der beiden Strahlengänge:
|
Aufgaben
Aufbauend auf dem Arbeitsblatt Verschmutzung der Meere C02-WS02-3) können Sie folgendes tun:
- Zeigen Sie bitte mit trigonometrischen Beziehungen und dem Snelliusschen Gesetz, dass für den geometrischen Wegunterschied Δs der Wellen der oben angegebene Ausdruck zutrifft, in Abhängigkeit von der Dicke d der Ölschicht, der Brechzahl n des Öls, und dem Beobachtungswinkel α.
- Berechnen Sie bitte die Phasendifferenz der Wellen für eine Dicke zwischen 0 und 5 mm der Ölschicht in Stufen von 0.25 mm mit den folgenden Annahmen: f=34 GHz, nÖl=1,41, γ=50°. Berücksichtigen Sie auch den Phasensprung der an Punkt C reflektierten Welle. Bestätigen Sie Richtigkeit der Position der Maxima und Minima der Strahlungstemperaturkurven auf Seite 2 in der Ergänzung über das Mikrowellenradiometer.
Materialien
- Dieses Arbeitsblatt als druckbare rtf-Datei
- Ölverschmutzung und das Verhalten von Öl im Meer
- Flugzeuggestützte Meeresüberwachung
- Das Mikrowellenradiometer
Hintergrundinformationen
- Lehrbücher zur Optik; das Thema ist physikalisch das gleiche wie die Interferenz von Lichtwellen, die durch eine dünne planparallele Platte transmittiert oder an ihr reflektiert werden.