1. Lineare empirische Regressionsmodelle

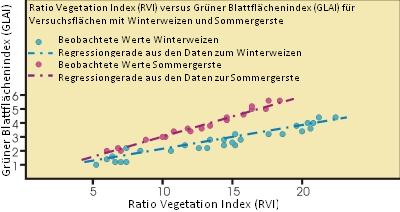
Beobachtungsdaten könnten ähnlich wie die in der Abbildung unten dargestellten Punkte aussehen, die dieser Datei entnommen wurden. Wenn Sie die Datei öffnen und die Daten in ein Tabellenblatt einfügen, können Sie ein Diagramm wie das unten gezeigte erstellen, allerdings ohne rote und blaue Regressionsgeraden.

Der Ratio Vegetation Index (RVI) aufgetragen gegen den Grünen Blattflächenindex (Green Leaf Area Index, GLAI) für Versuchsflächen mit Winterweizen und Sommergerste.

Man erkennt, dass die Daten stark korreliert sind. Sie liegen nicht genau auf einer Linie, werden aber angemessen durch eine Linie repräsentiert. Da eine Gerade eine gute Annäherung an den Datenverlauf ergibt, werden wir ein lineares Regressionsmodell verwenden. Um den Blattflächenindex (GLAI) mit Hilfe des Ratio Vegetation Index (RVI) abzuschätzen, nutzen wir diese Beobachtungsdaten zur Erstellung des Modells.

Ein lineares Modell besitzt die Form

y= b 1 ·x+ b 0

b0 wird auch als Grundwert bezeichnet oder als konstante Verschiebung der abhängigen Variable entlang der y-Achse (in diesem Fall dem Grünen Blattflächenindex). b1 wird als Zuwachs zwischen den beiden Variablen bezeichnet.

In dieser Gleichung gibt es zwei Unbekannte, den Zuwachs und die Verschiebung. Daher könnte man die Gleichung lösen, wenn wir zwei Werte für den RVI und die entsprechenden beiden Werte für den GLAI hätten.

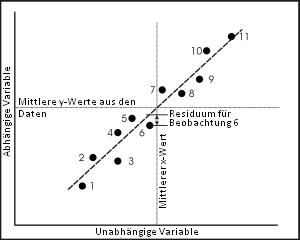
The concept of linear regression
Das Konzept der linearen Regression.

In der Datei haben wir aber noch viel mehr als nur zwei Beobachtungen, nämlich 53 für die Sommergerste und 62 für den Winterweizen. Außerdem liegen die Daten nicht genau auf der Geraden, sodass es für jeden beobachteten Wert der unabhängigen Variable, d.h. den x-Wert (RVI), unwahrscheinlich ist, dass der Wert der abhängigen Variable, der y-Wert (GLAI), genau auf der Geraden liegt. Vielmehr liegt er ein kleines Stück von der Geraden entfernt. Diese Abweichung in Richtung der y-Achse nennt man Residuum und sie wird in der Gleichungen mit dem Symbol ε angegeben.

y= b 1 ·x+ b 0 +ε

In Übereinstimmung mit einigen Kriterien müssen wir einen Weg finden, die Zuwachs- und Verschiebungswerte für diejenige Gerade zu finden, welche die beste Annäherung an die Daten liefert. Das übliche Kriterium hierfür ist, dass die Summe der Quadrate der Residuen minimal ist. Das ist als würden wir sagen, dass wir die Gerade finden wollen, die mit der kleinstmöglichen Varianz in y-Richtung zu unseren Daten passt. Die dafür von uns eingesetzte Methode wird als Methode der kleinsten Quadrate bezeichnet, welche Sie im nächsten Kapitel kennenlernen.

Aufgaben

  1. Öffnen Sie diese Datei und fügen Sie die Daten in ein Tabellenblatt ein. So erhalten Sie vier Spalten mit Daten, den RVI- und GLAI-Daten für Winterweizen und Sommergerste. Erstellen Sie ein Diagramm mit Graphen für beide Getreidearten, wobei die zwei Datensätze verschiedenfarbig dargestellt sein sollen.

  2. Berechnen Sie für jede Spalte den Mittelwert und die Varianz sowie die Korrelation zwischen den beiden Variablen sowohl für den Winterweizen als auch für die Sommergerste.