2. La méthode de régression par les moindres carrés (2/2)

La solution de ces deux équations devient relativement facile à trouver en écrivant les N équations d'observations sous une forme matricielle en plaçant les différentes valeurs de x et y correspondantes et les deux inconnues b1 et b0 dans des matrices.

[ x 1 x 2 . . . x N ]⋅[ b 1 b 0 ]=[ y 1 y 2 . . . y N ]   ou   O·U=B ,

O , U et D sont les trois matrices ci-dessus. Si l'on multiplie les deux membres de l'équation matricielle à gauche (la multiplication matricielle n'est pas commutative !!!) par la transposée de la première matrice, on obtient

O T ·T·U= O T ·D

ou A·U=B , appelée l'équation normale. On peut facilement démontrer que l'équation A·U=B a la même forme que les équations précédentes.

Dès lors, U= A −1 ·B où A −1 est l'inverse de la matrice A .

Pour une régression linéaire simple, la matrice A est une matrice (2,2), U est une matrice (2,2), et B une matrice (2,1). De cette manière, l'équation normale peut être résolue directement, sans inverser A . Les deux équations normales sont

b 1 ∑ x 2 + b 0 ∑ x= ∑ xy b 1 ∑ x+ N b 0 = ∑ y

D'où nous pouvons trouver b1 et b0

b 1 = N ∑ xy− ∑ x ⋅ ∑ y N ∑ x 2 − ( ∑ x ) 2 b 0 = ∑ y ⋅ ∑ x 2 − ∑ x ⋅ ∑ xy N ∑ x 2 − ( ∑ x ) 2

Avec

y ˆ = b 0 + b 1 ⋅x

Où ŷ est une estimation de y et non sa véritable valeur, de laquelle il diffère du résidu de la paire d'observations.

values returned by the Excell LINEST function
Explication des valeurs données par la fonction DROITEREG d'Excel.
Source: Microsoft 2003

Vous pouvez importer les données contenant les valeurs de RVI et de GLAI rassemblées en paires pour le blé d'hiver et l'orge de printemps dans un tableur, et utiliser les fonctions de sommation de votre tableur pour calculer la somme des x et des y, la somme des x2 et y2 et la somme de produits xy dans des cellules de votre feuille de calcul, et ensuite résoudre les deux inconnues. Une fois ceci fait pour un type de plantation, copiez les cellules afin de faire la même chose pour l'autre.

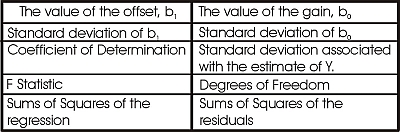
Une fois cela fait, testez la fonction DROITEREG d'Excel (LINEST en anglais). Pour utiliser DROITEREG, sélectionnez une cellule dans le coin supérieur gauche d'une plage de dix cellules (2 colonnes et 5 lignes) vides. Insérez-y la fonction DROITEREG en spécifiant les valeurs de ses 4 paramètres, le vecteurs des y (GLAI), celui des x (RVI), Vrai et Vrai pour les deux dernier paramètres à encoder. Ensuite, sélectionnez la plage des dix cellules, puis dans la fenêtre contenant la fonction DROITEREG, sélectionnez cette dernière et pressez simultanément Ctrl-Shift-Enter pour que la fonction remplisse les dix cases sélectionnées. L'aide sur la fonction DROITEREG expliquera la signification de ces dix valeurs qui est aussi donnée dans le tableau ci-dessus.

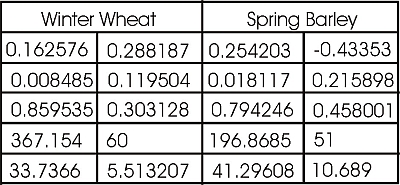
Pour ces deux groupes de données, vous devriez obtenir les valeurs comme montrées dans le tableau ci-dessous.

Résultats de l'ajustement d'un modèle linéaire par régression par moindres carrés aux données pour le blé d'hiver et l'orge de printemps.

Exercices

  1. Utilisez le fichier de données de la leçon précédente et ouvrez-le dans un tableur, ou reprenez la feuille de calcul créée au cours de la leçon précédente. Estimez les paramètres de la régression linéaire en calculant la somme de x et des y, celle des x2 et des y2 et celle des produits xy à l'aide des fonctions de sommation du tableur (SOMME, SOMME.CARRES, SOMMEPROD, par exemple). Assurez-vous que vous avez sélectionné les colonnes correctes. Ensuite, calculez les paramètres de la régression en utilisant les équations appropriées expliquées précédemment dans la leçon.

  2. Utilisez la fonction DROITEREG pour faire le même travail. Vous pouvez trouver les deux valeurs des paramètres dans le résultat de DROITEREG, mais ces résultats contiennent bien plus d'information dont nous reparlerons aux cours des prochaines leçons.

  3. Sur le diagramme de dispersion, sélectionnez des points d'un des deux jeux de données. Un menu pop-up devrait apparaitre. Dans ce menu, choisissez " Ajouter une courbe de tendance ", choisissez le type " linéaire " et assurez-vous que l'équation et le R2 apparaitront sur le graphique.

  4. Utilisez vos équations de régression pour entrer les valeurs résiduelles de chaque observation dans les deux jeux de données. Créez un graphique des résidus et estimez leur moyenne et leur variance. Que remarquez-vous à propos de la moyenne et de la variance ?