3. Interpretation des Modells der linearen Regression (1/2)
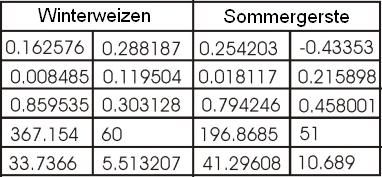
Öffnen Sie das bereits von Ihnen erstellte Tabellenblatt oder erstellen Sie eines mit Daten aus dieser Textdatei. Zeichnen Sie für jede der Getreidearten eine Regressionsgerade. Was können wir an den Regressionsgeraden ablesen? Zunächst zum Verschiebungswert b0: dabei handelt es sich um den Y-Wert, der vorliegt, wenn X = 0 ist. Es ist also der Y-Wert an der Stelle, an der die Gerade die Y-Achse schneidet.
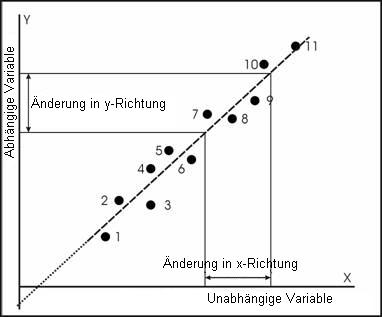
Der zweite Parameter, auch als Zuwachs bezeichnet, gibt die Steigung der Geraden an, oder das Verhältnis der Änderung des Y-Wertes zur Änderung des X-Wertes. Diese Steigung ist positiv, wenn die Gerade in die Richtung steigt, wie in der Abbildung links unten zu sehen; würde die Gerade von oben links nach unten rechts verlaufen, wäre die Steigung negativ.
Für jeden beobachteten X-Wert gibt es einen entsprechenden Y-Wert. Der Unterschied zu dem anhand der Regressionsgeraden abgeschätzten Y-Wert ist das Residuum. Außerdem wissen wir, dass die Quadratsumme der Residuen bei der angewandten Methode minimiert wird.
Die in der Tabelle und in Ihrem Tabellenblatt angegebenen Ergebnisse zeigen, dass die Sommergerste einen negativen Zuwachs zeigt, während der Winterweizen einen positiven Zuwachs aufweist. Außerdem ist die Gerade für die Sommergerste steiler, als die Gerade für den Winterweizen.
Wir haben nun die sich am Besten an unsere Daten annähernde Kurve gefunden, indem wir die kleinsten Quadrate als Kriterium verwendet haben. Trotzdem ist es normalerweise auch wichtig, herauszufinden, wie sehr man sich auf dieses Ergebnis verlassen kann. Können wir zum Beispiel beiden Ausgleichskurven gleichstark vertrauen oder ist eine von ihnen der anderen deutlich überlegen?