3. Interprétation du modèle de régression linéaire (1/2)
Ouvrez votre feuille de tableur de la leçon précédente, ou créez-en une nouvelle depuis le text file et construisez une droite de régression linéaire pour chaque type de culture. Que pouvons-nous déduire de ces droites de régression ? Premièrement, la valeur d'offset, 0 est la valeur d'Y quand X = 0, c'est donc la valeur de Y quand la droite croise l'axe Y (ordonnée à l'origine).
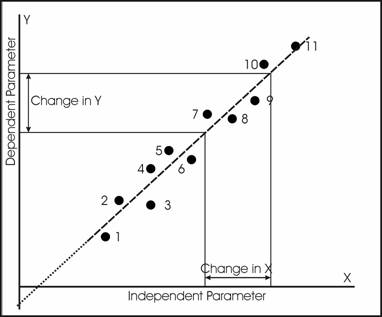
Le second paramètre, le gain, correspond à la pente de la droite, ou le rapport de variation de Y à variation de X. Cette pente est positive quand la droite est inclinée comme montré dans la figure ci-dessous. Si la droite était inclinée depuis le coin supérieur gauche vers le coin inférieur droit, la pente serait négative.
Nous savons que chaque valeur de X observée a une valeur de Y associée, et que la différence entre cette valeur et la valeur de Y estimée par la droite de régression est son résidu. La somme des carrées de ces résidus est minimisée dans ce processus.
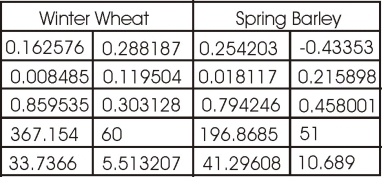
Le résultat donné dans le tableau suivant et dans votre feuille de tableur montre que l'orge de printemps a un intercepte négatif, alors que celui du blé d'hiver est positif. De plus, la pente de la droite de l'orge de printemps est plus forte que celle de la droite de blé d'hiver.
Maintenant, nous avons trouvé la meilleure courbe s'ajustant à une ligne grâce au critère des moindres carrés. Quoi qu'il en soit, il est aussi important de savoir la confiance que l'on peut accorder au résultat. Par exemple, pouvons-nous accorder la même confiance aux deux ajustements linéaires ou l'un est-il significativement supérieur à l'autre ?