3. Interpretation des Modells der linearen Regression (2/2)
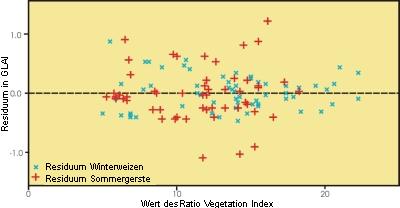
Ein erster Schritt bei der Auswertung ist es, sich die Residuen anzusehen, wie in der Abbildung unten dargestellt. Die genaue Prüfung der Residuen lässt vermuten, dass es ein Muster in ihrer Verteilung für den Winterweizen gibt. Auf der rechten Seite ist erst eine leichte Abnahme in den Werten zu erkennen und dann ein geringer Anstieg. Dies ist zwar nicht sehr deutlich sichtbar, verleitet jedoch zu der Annahme, dass ein Polynom höherer Ordnung eventuell eine bessere Annäherung an die Daten ergeben könnte.
Die Residuen für die Sommergerste zeigen andererseits kein signifikantes Muster, obwohl es ein paar große Ausreißer gibt. Obwohl ein Polynom zweiter Ordnung beim Winterweizen etwas kleinere Residuen liefert, soll hier weiterhin die lineare Regression genutzt werden. Im folgenden Kapitel betrachten wir die Güte der Ausgleichsgeraden nach dem linearen Modell.
Aufgaben:
- Finden Sie die quadratische Polynomfunktion, welche die Daten am Besten annähert. Bedenken Sie dabei, dass die quadratische Funktion folgende Form besitzt: b2X2+b1X+b0=Y+ε, es müssen also drei Unbekannte gefunden werden.
- Wiederholen Sie diesen Vorgang, aber markieren Sie dafür einen Datensatz auf dem Graphen und wählen Sie Trendlinie hinzufügen in dem Pop-up-Menü, das auftaucht, wenn Sie einen Punkt des Datensatzes anklicken. Wählen Sie eine Polynomfunktion zweiter Ordnung und lassen Sie sich die Funktionsgleichung und den R2-Wert in dem Diagramm anzeigen.