3. Interprétation du modèle de régression linéaire (2/2)

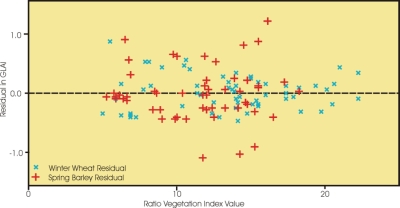
La première étape de cette analyse est de regarder les résidus, comme montré ci-dessous. La lecture de ces résidus suggère une certaine tendance pour les résidus du blé d'hiver, avec une légère diminution des résidus suivie d'une légère augmentation à la droite du graphe. Ce n'est pas évident, mais cela suggère bien qu'un polynôme d'ordre supérieur pourrait apporter un meilleur ajustement aux données.

Résidus de la fonction de régression linéaire aux données de la table 1

Les résidus de l'orge de printemps ne montrent quant à eux aucune tendance significative, bien qu'il y ait quelques points largement à l'écart. Bien qu'un polynôme de second ordre donne en effet des résidus moindres pour le blé d'hiver, continuons à nous focaliser sur la régression linéaire en passant à la leçon suivante pour étudier la qualité de chaque ajustement de modèle linéaire.

Exercices:

1. Trouvez le meilleur ajustement de fonction polynomiale quadratique aux données, en vous rappelant qu'une fonction quadratique a la forme b₂X²+b₁X+b₀=Y+ε de manière à ce que trois inconnues doivent être trouvées.


2. Répétez le processus, mais sélectionnez un jeu de données dans le graphe et sélectionnez Add Trendline dans le menu pop-up qui apparait quand vous cliquez sur un point du jeu de données. Sélectionnez " fonction polynomiale du second ordre " et faites afficher l'équation et la valeur du R au carré sur le graphe.