7. Modèles Stochastiques et Déterministes (2/2)

La raison de ce phénomène est que l'attraction gravitationnelle entre la Terre et la lune n'est pas assez forte pour la garder sur une orbite fixe. Au fur et à mesure que la distance entre la terre et la lune augmente, la force gravitationnelle diminue et donc la distance entre les deux augmente plus rapidement, toute chose étant égale par ailleurs. En pratique, toute chose n'est pas égale par ailleurs, et la vitesse de la lune va diminuer, et donc la force centrifuge se réduire.

Une autre classe de modèles déterministes est utilisée dans l'étude des populations animales. Les modèles initiaux de croissance de population étaient basés sur l'idée de croissance exponentielle selon laquelle l'augmentation de population par unité de temps est fonction de la taille de la population à ce moment et du taux de croissance de la population.

N1 = N0 · R
Nt = N0 · Rt

Où N0 est la population de départ, N1 la première génération, R vaut (1,0 + le taux de croissance), et Nt est là tième génération.

Considérons la division cellulaire. Chaque cellule se divise en deux à chaque génération, donc R = 2. Si la première génération a une cellule, alors la seconde devrait en avoir deux, la troisième devrait en avoir quatre, la quatrième huit, et ainsi de suite. C'est une croissance exponentielle.

Quoi qu'il en soit, les données expérimentales ont montré que bien que cela soit vrai sous certaines conditions, ça ne s'applique pas dans d'autres conditions. Cette observation amène à la conclusion que les populations deviennent limitées, retenues lorsqu'elles atteignent une certaine taille, par l'espace ou la nourriture disponible par exemple, et que cela réduit le taux de croissance de la population. Cela a amené à une autre génération de modèles de croissance de population, basés sur la courbe logistique.

N t = N o K N o +(K− N o )⋅exp(− r 0 t)

Où K est la limite maximum de la population, souvent appelée capacité de support, et ro = R - 1.

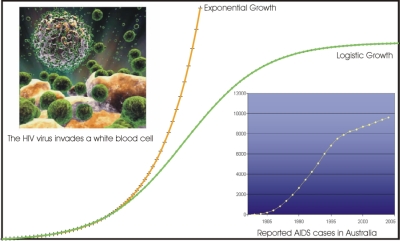
La courbe exponentielle, la courbe logistique, et l'application de la fonction logistique à la propagation du Sida en Australie.
Source: Murray Bourne, 1997-2009

Le virus du SIDA a été introduit dans une ville de 50 000 habitants qui ne prenaient aucunes précautions par 100 personnes. Après 10 semaines, il a été observé que 1 000 personnes étaient infectées. En supposant que l'épidémie suit la courbe logistique, combien de temps faudra-t-il pour que la moitié de la population soit affectée ?

Utilisez l'équation ci-dessus avec les données que vous avez reçues, et sachant que t = 10 semaines, trouvez ro = 0,23208. Ensuite, utilisez ce taux dans l'équation ci-dessus pour trouver que la moitié de la population sera infectés après 26,8 semaines, ou à peu près 27 semaines.

Questions

  1. Quelle est la force gravitationnelle entre vous et la terre ? Vous n'avez pas besoin de la calculer, ou si vous le faite, la réponse serait exactement la même que votre poids. Votre poids est une mesure de cette force.

  2. Quel est votre poids sur la lune ? répondez d'abords à cette question en utilisant la loi de la gravitation, en la transformant en un rapport de la force gravitationnelle sur la Terre et sur la lune. Simplifiez ce rapport pour obtenir l'équation
    F Lune F Terre = M Lune M Terre ⋅ R Terre 2 R Lune 2
    La masse de la lune vaut 0,73483·1023 kg et son rayon est de 1738 km, la masse de la Terre est de 59,74·1023 kg et son rayon vaut 6371 km. La connaissance de votre poids sur la terre vous permet de le calculer sur la lune. Vérifiez votre réponse en allant à cette adresse.