1. Fundamentos físicos
Princípios da radiação (2/2)
A lei de radiação de Planck
Em 1900, Max Planck introduziu o conceito de propriedades quantizadas de luz, ou seja, os fótons, que se tornou um ponto de partida da teoria quântica. No quadro da física clássica e com base em ondas electromagnéticas que não tinha sido possível compreender a física da radiação térmica. Usando o conceito de fótons, Planck derivada uma equação que descreve a intensidade e forma espectral da radiação térmica de um corpo negro ideal emissor. Omitindo algumas constantes físicas, lê-se:
Onde λ é o comprimento de onda de emissão e T é a temperatura absoluta. E h=6.68·10-34 Ws2 é a constante de Planck, c é a velocidade da luz, e k=1.38·10-23 Ws/K é a constante de Boltzmann.
Obviamente, os espectros de emissão de um corpo negro ideal dependerá da sua temperatura apenas, e as propriedades do material não interferem. Lei de Planck é valida para sólidos, líquidos e gases. Exemplos da curvas de Planck são apresentados no gráfico à direita. Os espectros de emissão de corpo cinzento pode ser calculada usando a sua eficiência de emissão espectral, isto é,ελMλ.
Lei do deslocamento de Wien
Em 1893, Wilhelm Wien descreveu uma uma equação que permitiu calcular o comprimento de onda máximo λmax de um espectro de emissão de corpo negro em função da temperatura T:
sendo o valor da constante 0,30 cm K. Assim, altas temperaturas correspondem a valores máximos de comprimento de onda baixa e vice-versa.
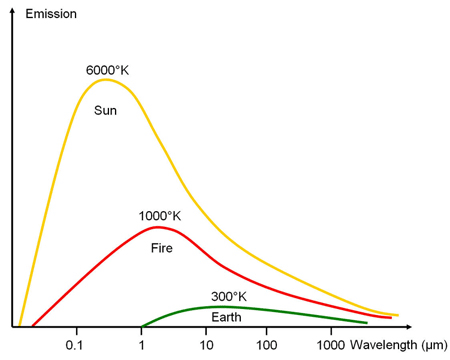
Fonte: ESA Eduspace com modificações
O sol com sua alta de temperatura superficial de cerca de 6.000 K emite luz visível que tem um máximo de aproximadamente λmax=0,5 µm. A Terra com uma temperatura ambiente de 300 K emite predominantemente no infravermelho médio com um máximo de cerca de 10 µm; o que é chamado de faixa espectral do infravermelho termal.
