2. Mit Zeitreihen arbeiten
Mauna Loa-Zeitreihe des Kohlendioxids in der Atmosphäre (2/5)
Der Trend
Zur Bestimmung des Trends berechnen wir zunächst die Jahres- mittelwerte des Datensatzes. Dann passen wir eine nichtlineare Funktion an die Daten an, indem wir die Methode der kleinsten Quadrate anwenden. Wie dies geschieht, wird in der SEOS-Lerneinheit Umweltmodellierung erklärt. Die Verwendung von Ausgleichsgeraden - also linearen Funktionen - wurde auf den vorherigen Seiten des Kapitels erarbeitet.
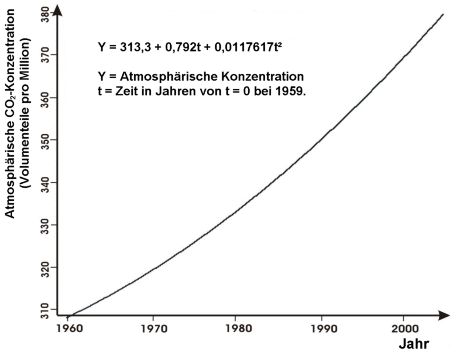
Die Gleichung der Parabel ist
wenn wir t = 0 für das Jahr 1959 setzen. Der Korrelationskoeffizient mit den Messdaten ist r=0,993. So sehen wir, dass mit einem Startwert von 313,3 Teilen pro Million in 1959 das atmosphärische Kohlendioxid im Zeitverlauf ansteigt und die Anstiegsrate ebenfalls wächst.
Warum haben wir eine Parabel gewählt?
Es gibt viele verschiedene Funktionstypen, die man wählen könnte, beginnend mit einer einfachen Gerade. Eine Geradengleichung liefert eine konstante Anstiegsrate. Doch bei unserer Datenerhebung steigt die Anstiegsrate im Zeitverlauf.
Eine Parabel scheint die einfachste Funktion zu sein, die zu unseren Daten passt. Aber andere Funktionen könnten möglicherweise zu besseren Ergebnissen führen. Welche Funktion wir wählen, sie kann uns jedoch keinen Hinweis auf die Ursache des Trends geben, den man in den Daten erkennt.
In jedem Fall wird die Parabel ohne Zusatzinformationen das passendste einfache Modell sein, das wir zur Berechnung der aktuell stattfindenden Veränderungen benutzen können.
Was bleibt übrig?
Die folgende Graphik zeigt uns die Schwankungen, die nach der Herausnahme der Parabelwerte zurück bleiben.
Die Kurve verhält sich stark periodisch, doch man kann noch mehr feststellen. Es gibt längerfristige Schwankungen, die nicht in eine bestimmte Richtung verlaufen. (Übrigens, diese Restschwankungen umfassen ein Intervall von 4,997 bis -4,753 ppmv).
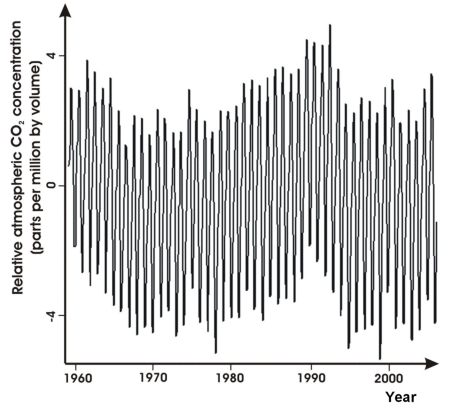
Um dem nachzugehen, werden wir im nächsten Schritt die jahreszeitlichen Schwankungen entfernen.
