2. Mit Zeitreihen arbeiten
Mauna Loa-Zeitreihe des Kohlendioxids in der Atmosphäre (4/5)
Periodische Signale
Eine Möglichkeit, periodische Komponenten in einer Zeitreihe zu finden, besteht im Umwandeln der Messwerte in einen Graphen, der die Anteile der Daten bei jeder Frequenz anzeigt, die in der Zeitreihe enthalten ist. Wir nutzen hierfür die Fourier-Transformation.
Bei der Fourier-Transformation wird angenommen, dass eine Datenreihe aus periodischen Funktionen zusammengesetzt ist, beispielsweise aus Sinus-Funktionen unterschiedlicher Frequenz. Die Fourier-Transformation überführt die Daten vom Zeitbereich in den Frequenzbereich. Dort werden die im Ausgangsdatensatz vorhandenen Frequenzen und die Amplituden der Sinus-Funktionen mit diesen Frequenzen anzeigt; man nennt dies ein Frequenzspektrum.
Wir werden die sogenannte Diskrete Fourier-Transformation benutzen, in der die Details, die wir aus der Datenmenge filtern können, von der Zahl der Messwerte und ihrem zeitlichen Abstand abhängen.
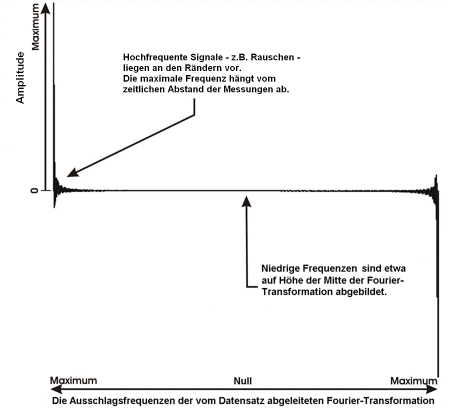
Die Werte am linken und rechten Ende der Grafik zeigen die Werte bei hohen Frequenzen, die dem Rauschen im Datensatz entsprechen.
Es treten nur geringe Werte bei kleinen Frequenzen auf, da das Signal im mittleren Bereich sehr flach ist. Ein zusätzliches Filtern der Daten führt hier zu keinem besseren Ergebnis.
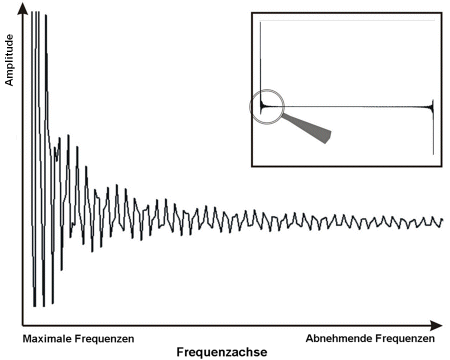
Lassen Sie uns einen genaueren Blick auf die äußeren Ränder des Graphen werfen, um zu erkennen, wie er tatsächlich aussieht.
Was passiert, wenn wir das Rauschen beseitigen?