2. Mit Zeitreihen arbeiten

Mauna Loa-Zeitreihe des Kohlendioxids in der Atmosphäre (5/5)

Periodische Signale (Fortsetzung)

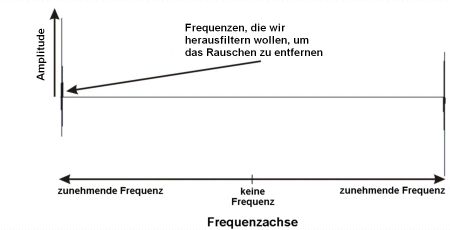
Wir nutzen nun das Frequenzspektrum, um das Rauschen von anderen periodischen Komponenten zu trennen.

Rauschen ist als zufällige Schwankung definiert, die von Messung zu Messung in einer Untersuchung auftritt. In unserer Frequenzanalyse sollte dies nur in den sehr hochfrequentierten Bereichen auftreten; hohe Frequenzen entsprechen kleinen Zeitperioden, und kürzere Zeiten als diejenigen von Messung zu Messung treten nicht auf.

Die im nächsten Graphen gezeigten Frequenzen werden durch Filtern aus dem Frequenzspektrum entfernt, wodurch das Rauschen verringert wird.

Frequenzen, die aus dem Spektrum entfernt werden.

Sind diese Frequenzen entfernt, so wird das verbleibende Spektrum durch die inverse Fourier-Transformation wieder in den Zeitbereich übertragen.

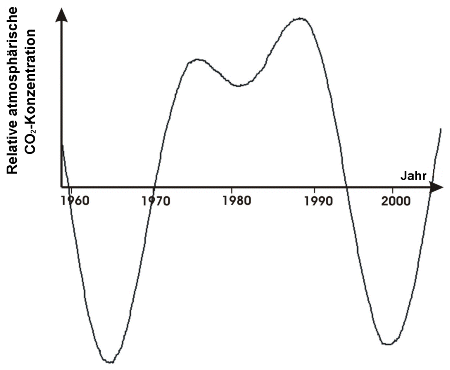
Dadurch erhalten wir das unten gezeigte Ergebnis. Die Grafik zeigt die rauschbefreiten Anteile mit nicht-jährlicher Periodendauer im Datensatz.

Die Kurve der Restgrößen, die nach der Filterung der hohen Frequenzen verbleiben. Es fällt sicherlich auf, dass die Kurve sehr viel glatter verläuft als der Ursprungsgraph der Restgrößen vor der Filterung, der zwei Seiten zuvor gezeigt wurde.

Wir können nun dieses geglättete Signal von dem - zwei Seiten zurück gezeigten Signal abziehen, welches noch das Rauschen enthielt.

Die Restfunktion, nachdem die geglättete Funktion von der Ausgangsfunktion abgezogen wurde, mit der die Fourier-Analyse begonnen wurde. Diese Daten weisen immer noch eine gewisse Struktur auf.

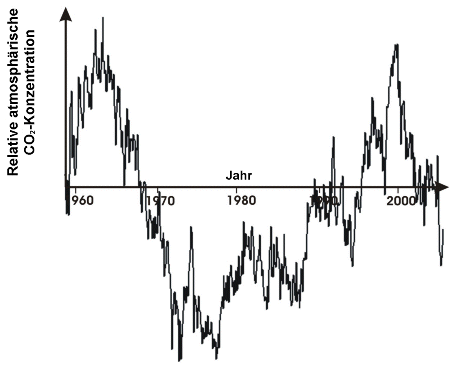
Was denken Sie hierüber? Enthält dies immer noch periodische Anteile? Es scheint so, auch wenn sie sehr gering sind. Hätten wir vielleicht nur die Anteile bei der höchsten Frequenz durch Filterung entfernen sollen?