Ergänzung 2.1: Punktwolken und Ausgleichsgeraden (1/3)

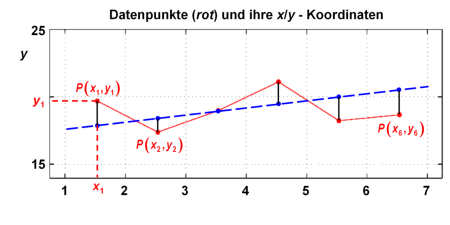
Wir betrachten eine Punktwolke aus i=1...n Datenpunkten $P(x_i,y_i)$ , wobei n eine natürliche Zahl ist (Grafik links unten). Gesucht ist die Gerade, welche die beste Annäherung für die Verteilung der Datenpunkte darstellt. Hierzu untersuchen wir die Gleichung einer Geraden (in den Grafiken als blaue gebrochene Linie eingezeichnet),

und insbesondere die Punkte $P(x_i,f(x_i))$ auf dieser Geraden mit gleichen x-Koordinaten wie die Datenpunkte (Grafik rechts unten; zum Umschalten auf die jeweilige Überschrift klicken).

Punktwolke P(x_i,y_i) Gerade und projezierte Punkte P(x_i,f(x_i))

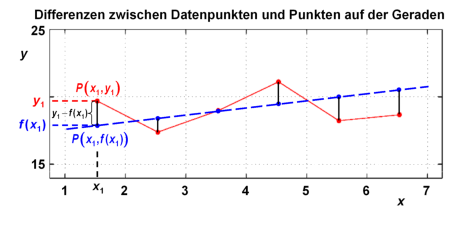
Die Differenzen zwischen den Datenpunkten und den Punkten auf der Geraden mit gleichen x-Werten sind durch $y_i-f(x_i)$ gegeben. Diese Differenzen, in der unten abgebildeten Grafik am Beispiel der Punkte $P(x_1,y_1)$ und $P\left(x_1,f(x_1)\right)$ gezeigt, erlauben es, die Gerade zu finden, mit der die Datenpunkte am besten wiedergegeben werden. Diese Ausgleichsgerade sollte kleinstmögliche Abstände zu den Datenpunkten aufweisen, d.h. die Differenzen ein Minimum einnehmen!

Alternativ könnte man auch die Differenzen zwischen den Datenpunkten und den Punkten auf der Geraden mit gleichen y-Werten untersuchen. Dies bezeichnet man als Regressionsanalyse bezüglich y.

Im weiteren betrachten wir eine Regressionsanalyse bezüglich x.

Es wäre nicht sinnvoll, die Differenzen aufzuaddieren und das Minimum durch Ändern der Lage der Geraden zu suchen, da diese Differenzen positiv und negativ sind. Auf das Vorzeichen soll es nicht ankommen. Daher werden die Differenzen quadriert, und wir bestimmen die mittlere quadratische Abweichung

in unserem Beispiel:                           $S=\frac{{\left(y_1-f(x_1)\right)}^2+\mathrm{...}+{\left(y_6-f(x_6)\right)}^2}{6}$

Ersetzt man $f(x_i)$ durch $f(x_i)=a{x}_i+b$, so folgt:

mit der Steigung a und dem y-Achsenabschnitt b der Geraden.

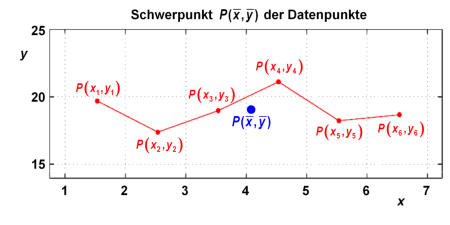
Der Schwerpunkt der Datenpunkte

Die Ausgleichsgerade ist gefunden, wenn die Parameter a und b der Geraden so gewählt sind, dass die mittlere quadratische Abweichung

ein Minimum einnimmt. Daher berechnen wir die Ableitung von S und setzen sie zu Null.

Allerdings hängt S von zwei Variablen ab, a und b. Daher bestimmen wir die Ableitung in zwei Schritten. Wir leiten zunächst S nach b ab und halten a konstant. In einem zweiten Schritt leiten wir S nach a ab und halten b konstant. (In der höheren Differenzialrechnung bezeichnet man S als Funktion zweier Variabler, und wir berechnen die parziellen Ableitungen von S nach den Variablen a bzw. b)

Die Ableitung nach b ergibt:

Mit              $\frac{1}{n}\sum _{i=1}^n{y}_i=\overline{y}\frac{1}{n}\sum _{i=1}^n{x}_i=\overline{x}\frac{1}{n}\sum _{i=1}^{n}b=b$

wobei $\overline{x}$ und $\overline{y}$ die arithmetischen Mittelwerte der $x_i$- und $y_i$ -Koordinaten sind, folgt:

Das Minimum von $S(b)$ ergibt sich aus $S\text{'}(b)=0$, und man erhält:

Dies sieht zunächst aus wie eine Geradengleichung. Allerdings sind die Mittelwerte $\overline{x}$ und $\overline{y}$ Koordinaten eines Punktes. Der Punkt $P(\overline{x},\overline{y})$ ist daher das arithmetische Mittel der Punkte $P(x_i,y_i)$, er wird als Schwerpunkt bezeichnet.

Schwerpunkt $P(\overline{x},\overline{y})$ der Datenpunkte.