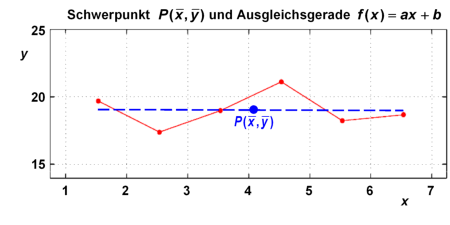
Ergänzung 2.1: Punktwolken und Ausgleichsgeraden (2/3)

Ausgleichsgeraden durch den Ursprung

Nun leiten wir $S (a, b)$ nach a ab.

Zur Vereinfachung betrachten wir eine Punktwolke mit einem Schwerpunkt $\bar{P} (\bar{x}', \bar{y}')$ im Ursprung eines $(x', y')$ -Koordinatensystems. Da der Schwerpunkt auf der Ausgleichsgeraden liegt, wird somit b=0 und

S (a) = \frac{1}{n} \sum_{i = 1}^{n} {(y_{i}^{'} - a x_{i}^{'})}^{2}

Ableiten: $S' (a) = \frac{2}{n} (a \sum_{i = 1}^{n} x_{i}^{2}' - \sum_{i = 1}^{n} x_{i}^{'} y_{i}^{'})$

und $S' (a) = 0$ setzen ergibt:

a = \frac{\sum_{i = 1}^{n} x_{i}^{'} y_{i}^{'}}{\sum_{i = 1}^{n} x_{i}^{2}'}

wobei $\sum_{i = 1}^{n} x_{i}^{2}' \neq 0$ erfüllt sein muss.

Wir betrachten n Punkte

P (x_{1}^{'}, x_{1}^{'}), ... P (x_{n}^{'}, x_{n}^{'})

mit einem Schwerpunkt

\bar{P} (\bar{x}', \bar{y}')

im Ursprung des Koordinatensystems. Dann verläuft die Ausgleichsgerade

y' = a x'

durch den Ursprung und hat die Steigung:

a = \frac{\sum_{i = 1}^{n} x_{i}^{'} y_{i}^{'}}{\sum_{i = 1}^{n} x_{i}^{2}'}

Ausgleichsgeraden mit y-Achsenabschnitt b

Wir setzen $x_{i}^{'} = x_{i} - \bar{x}$ und $y_{i}^{'} = y_{i} - \bar{y}$ , was einer Verschiebung der Koordinaten entspricht: die neuen (x,y)-Koordinatenachsen sind um $(\bar{x}, \bar{y})$ gegenüber den $(x', y')$ -Koordinaten, die in der linken Spalte genutzt worden sind, verschoben.