Supplement 2.1: Point Clouds and Linear Regression Lines (2/3)
Best-fit straight lines passing through the origin
Our next step is to differentiate with respect to a.
For simplicity, we consider a point cloud with a centroid in the origin of an coordinate system. Since the centroid is a point on the regression line, one has b=0 and
Differentiated:
and setting yields:
,
where is a necessary condition.
We consider n points
,
their centroid
lying in the origin of the coordinate system. Then the best-fit line
is passing through the origin and has the slope:
is passing through the origin and has the slope:
Best-fit straight lines with intercept b
We set and which corresponds to a shift of coordinates, the new (x,y) coordinate axes being shifted by with respect to the coordinates used in the left column.
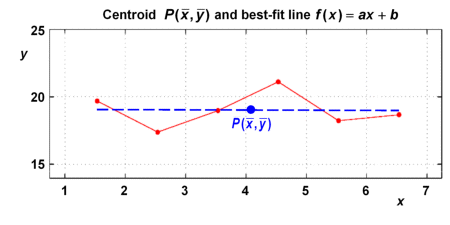
We consider n points with a centroid at .
It follows:
The slope of a best-fit line for a point cloud
having its centroid at point
is:
Since the centroid is lying on the best-fit line, once can use the point-slope form of straight lines to calculate:
The intercept follows from:
Since the centroid is lying on the best-fit line, once can use the point-slope form of straight lines to calculate:
The intercept follows from: