2. Einführung in die mathematischen Methoden
Wahrscheinlichkeitsdichtefunktionen
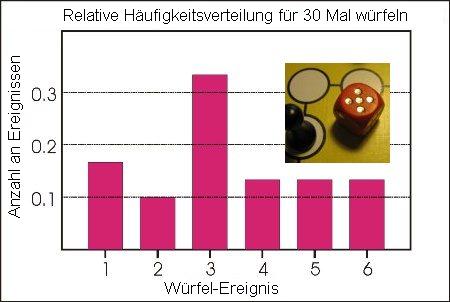
Wir haben Häufigkeitsverteilungen von Stichproben kennengelernt, aus denen ganz leicht Relative Häufigkeitsverteilungen erstellt werden können. Man kann Histogramme zeichnen, welche die Anteile der Würfe darstellen, die jede Augenzahl des Würfels ergeben haben. Die Wahrscheinlichkeitsdichtefunktion (WDF) einer Stichprobe ist eine relative Häufigkeitsverteilung, weil sie die Anteile der Wahrscheinlichkeit für das Eintreten jedes Ergebnisses aus der Stichprobe darstellt.
Wir wissen, dass die Wahrscheinlichkeit beim Würfeln für jede Augenzahl gleich groß ist, und zwar 1/6 für jedes mögliche Ergebnis. Wenn die Wahrscheinlichkeit für das Eintreten jedes Ergebnisses gleich ist, dann ist die Wahrscheinlichkeitsdichtefunktion der Daten gleichverteilt. Daher handelt es sich bei der theoretischen Verteilung beim Würfeln um eine Gleichverteilung mit dem Wert 1/6. Bei großen Stichprobenzahlen liegen die aus der Stichprobe abgeleiteten Wahrscheinlichkeiten nahe an der theoretischen Wahrscheinlichkeit.
Ermittelt man aus den Daten einer Stichprobe die Wahrscheinlichkeitsdichtefunktion, dann gilt sie streng betrachtet nur für diesen Datensatz. Meist sucht man aber eine Funktion, die auf viele Stichproben angewandt werden kann. Leitet man sie aus nur einer Stichprobe ab, kann die in einer Analyse signifikante Fehler verursachen und wird deshalb für die statistische Auswertung schwer nutzbar sein. Oft lässt sich eine geeignete Wahrscheinlichkeitsdichtefunktion entweder in Form einer theoretischen Verteilung oder als Annäherung an einen Datensatz finden.
Denken wir nochmal an einen Würfel. Theoretisch besteht für das Auftreten jeder Zahl die gleiche Wahrscheinlichkeit. Die theoretische Wahrscheinlichkeitsdichtefunktion für das Werfen eines Würfels ist also eine Gleichverteilung mit einem Wert von 1/6, sodass man bei 30 mal Würfeln jede Zahl 5 mal erhalten sollte. Bei der Stichprobe in Kapitel 1 ist dies jedoch nicht der Fall, da es sich um Daten aus einer ganz bestimmten Stichprobe handelt. Die theoretisch zu erwartende Gleichverteilung wird jedoch immer besser angenähert, je größer die Stichprobe ist.
| Wert | Anzahl Stichprobe | Wahrscheinlichkeit Stichprobe | Theoretische Wahrscheinlichkeit |
|---|---|---|---|
| 2 | 0 | 0,000 | 0,028 |
| 3 | 1 | 0,033 | 0,056 |
| 4 | 3 | 0,100 | 0,083 |
| 5 | 2 | 0,067 | 0,111 |
| 6 | 6 | 0,200 | 0,139 |
| 7 | 5 | 0,167 | 0,167 |
| 8 | 2 | 0,067 | 0,139 |
| 9 | 6 | 0,200 | 0,111 |
| 10 | 2 | 0,067 | 0,083 |
| 11 | 3 | 0,100 | 0,056 |
| 12 | 0 | 0,000 | 0,028 |
| Gesamt | 30 | 1,000 | 1,000 |
Die Wahrscheinlichkeitsdichtefunktion für den Wurf zweier Würfel ist keine Gleichverteilung. Wie kann man sie berechnen?
Die Wahrscheinlichkeit, eine zwei als Ergebnis zu erhalten, ist nur dann gegeben, wenn mit beiden Würfeln eine 1 geworfen wird. Wir wissen, dass die Wahrscheinlichkeit, mit einem Würfel eine 1 zu werfen, 1/6 beträgt. Daher ist die Wahrscheinlichkeit für das Werfen von zwei einsen (1/6)·(1/6) gleich (1/36). Eine 3 könnte man durch die Kombination einer 2 und einer 1 oder einer 1 und einer 2 erzielen. Für beide Ereignisse liegt die Wahrscheinlichkeit bei 1/36, sodass wir insgesamt eine Wahrscheinlichkeit von 2/36 haben. Die Werte für alle anderen Ergebnisse können Sie in der obenstehenden Tabelle nachsehen.
Wahrscheinlichkeitsdichtefunktionen von Stichproben sind für eine statistische Analyse von geringem Wert, weil nur eine begrenzte Zahl von Daten zur Verfügung steht und die Funktion sich jedes mal ändert, wenn eine neue Stichprobe erhoben wird. Für diskrete Ereignisse kann man oft die theoretische Wahrscheinlichkeitsdichtefunktion bestimmen, wie es hier für das Werfen eines und zweier Würfel gezeigt wurde. Für kontinuierliche Daten ist dies nicht immer möglich. Es gibt allerdings einige Standard-Wahrscheinlichkeitsdichtefunktionen, die sich in vielen Fällen als nützlich erwiesen haben. Im Folgenden werden wir auf zwei häufig verwendete Wahrscheinlichkeitsdichtefunktionen eingehen.