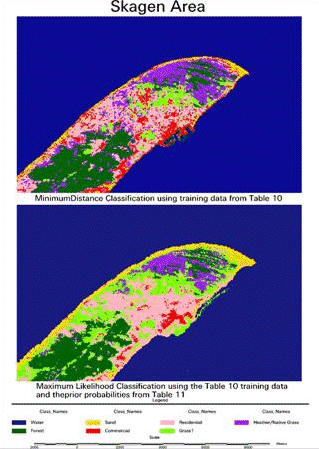
5. The Maximum Likelihood Classifier

Unlike the Minimum Distance Classifier, the Maximum Likelihood Classifier takes the variance and covariance into account.

Scattergram depicting three class means, their distribution in units of standard deviation, and class decision surfaces

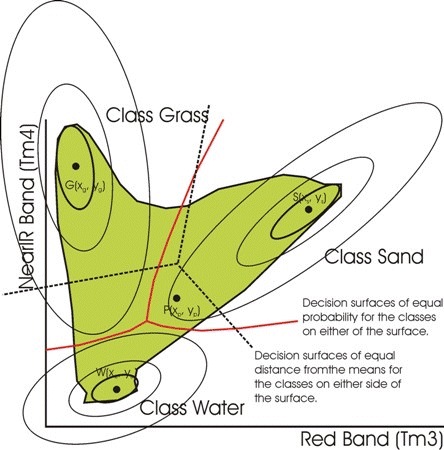
It does this by computing the distance from the pixel to each class mean value, in units of the standard deviation in that direction, and allocating the pixel to that class with the smallest value in these units of Mahalonobis distance.

Skagen area, minimum distance and maximum likelihood classification

Mahalonobis distances vary from class to class, and indeed from direction to direction within each class.

The Maximum Likelihood Classifier is based on Bayes Rule:

Where A_i represents class i, B represents the pixel response values.

Pr{A|B} is the conditional probability of Class A_i occurring given the pixel response values, Pr{A} are prior probabilities of class A_i occurring, and is the probability that the pixel values are in Class A_i. Conditional Probability has been described in Chapter 2.

In this equation the prior probabilities, Pr{A} are either made equal, or they are given values from prior mapping information. It is usual to assume that the data for a class is a good fit to the normal distribution, so each Pr{B|A} is computed using the Normal distribution as you have done in the Lesson on the Normal PDF. In this way pixel probabilities are computed from each class, and the pixel is assigned to that class for which it has the highest probability. Again, a minimum probability threshold can also be set, so that the pixel will not be assigned to any class if the probabilities are not higher than this threshold value.

Question:

The Minimum Distance Classifier is a special case of the Maximum Likelihood Classifier. What are these conditions that make the Minimum Distance Classifier a special case of the Maximum Likelihood Classifier?