Supplément 1.7: Grandeurs radiatives et radiométrie (4/5)

L'intensité énergétique ... suite de la page précédente

Pour un émetteur isotrope dont l'intensité du faisceau est indépendante de la direction, l'intégrale peut être résolue. Dans le cas d'un angle solide conique comme dans le graphique de la colonne de gauche de la page précédente, mais orienté vers le zénith, l'angle azimutal $φ$ varie de 0 à $2 π$ . L'angle zénithal $ϑ$ varie de 0 à la moitié de l'angle d'ouverture $ϑ'$ :

Φ = I \int_{ϑ = 0}^{ϑ'} \int_{φ = 0}^{2 π} sin ϑ d ϑ d φ = I \cdot 2 π (1 - cos ϑ')

Cette solution est une alternative au calcul présenté dans l'exemple Efficacité d'un collimateur à lentille à la page précédente.

Exercice 2 : Émetteurs isotropes ↓

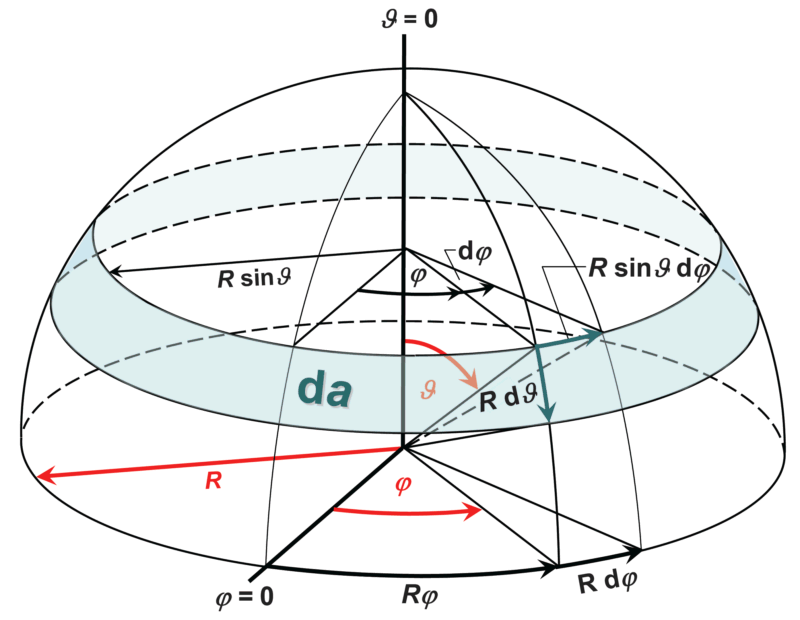
Dans le cas d'émetteurs anisotropes dont l'émission est symétrique autour d'un axe, l'intégrale peut être partiellement résolue. Pour cela, nous considérons le graphique suivant, dans lequel un angle solide axialement symétrique autour de l'axe vertical (l'axe zénithal) est représenté et apparaît comme une bande placée autour de l'hémisphère. Cet angle solide, également différentiel, est :

d Ω = \frac{d a}{R^{2}} = \int_{φ = 0}^{2 π} sin ϑ d ϑ d φ = 2 π sin ϑ d ϑ

En supposant que l'intensité du rayonnement $I (ϑ)$ dépend uniquement de l'angle zénithal ϑ, l'émission peut être intégrée par rapport à l'angle azimutal φ :

Φ = \int_{ϑ_{1}}^{ϑ_{2}} \int_{φ = 0}^{2 π} I (ϑ) sin ϑ d ϑ d φ = 2 π \int_{ϑ_{1}}^{ϑ_{2}} I (ϑ) sin ϑ d ϑ

Équations ↓

L'intégration sur l'angle azimutal φ de 0 à

2 π

donne une bande autour de la sphère sous l'angle zénithal ϑ avec une largeur Rdϑ. En raison de la largeur différentielle, cette bande est également un élément de surface différentiel da.

Exercice 3 : Émetteurs anisotropes ↓

L'intensité axialement symétrique d'une lampe est donnée par

I (ϑ) = \frac{1}{2} I (ϑ = 0) (1 + cos ϑ)

Veuillez esquisser la répartition de l'intensité sur l'angle zénithal ϑ de 0 à 180°.
Calculez le flux énergétique total émise en fonction de l'intensité du rayonnement pour ϑ = 0.

Vérifiez vos résultats sur cette page !

Les émetteurs cosinus ou émetteurs Lambert, nommés d'après le mathématicien et physicien Johann Heinrich Lambert (1728-1777), constituent une forme particulière d'émetteurs anisotropes. Ces émetteurs sont abordés dans le supplément 1.8.

Les méthodes de mesure de l'intensité énergétique sont présentées dans la section consacrée à la radiance.

Le spectre de la Terre

Supplément 1.7: Grandeurs radiatives et radiométrie (4/5)

L'intensité énergétique ... suite de la page précédente