Ergänzung 1.8: Lambert-Strahler, Kosinus-Strahler      (3/4)

Weitere Beispiele      ...Fortsetzung von der vorherigen Seite

Weiße Wände, weiße Glasscheiben      ...fortgesetzt

Nun kann man einwenden, dass der Abstand zur gesehenen Fläche gleich geblieben ist. Daher untersuchen wir nun die Situation bei gleich bleibendem senkrechtem Abstand zur Mattscheibe.

Zoom Sign
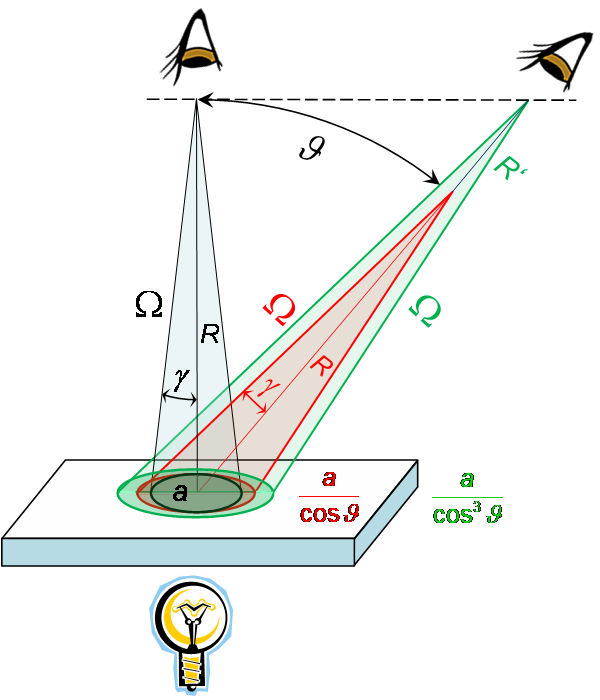
Mattglasscheibe unter verschiedenen Winkeln betrachtet
Der Betrachter beobachtet nun in einer Ebene parallel zur Matt­scheibe. Unter dem Beobachtungswinkel ϑ vergrößert sich der Ab­stand von R auf den Wert R'. Der Raumwinkel Ω soll gleich bleiben.
Gleichungen ↓

Für die Ansicht unter dem Winkel ϑ im bisherigen Abstand R gilt nach dem Ergebnis der vorherigen Seite (rot):

Ω=a/ ( R 2 cosϑ )

Im rechtwinkligen Dreieck gilt für den Abstand R':

cosϑ=R/ R'

Damit wird (grün):      Ω=a/ ( R ' 2 cos 3 ϑ )

Die betrachtete Fläche ist somit gegenüber der senkrechten Orientierung um den Faktor a/cos³ϑ gewachsen.

Andererseits lässt sich schreiben:

a/ cos 3 ϑ = R ' 2 R 2 ⋅ a cosϑ

Der Faktor R ' 2 / R 2 kompensiert gerade die nach dem photometrischen Entfernungsgesetz zu erwartende Abnahme der Bestrahlungsstärke (W/m²) mit dem Quadrat der Entfernung zur Lichtquelle. Dies muss so sein, andernfalls bliebe die Strahlstärke nicht erhalten.

Die unter festem Raumwinkel mit dem Auge beobachtete Strahlstärke bleibt demnach auch mit veränderlicher Entfernung zur leuchtenden Fläche erhalten.