Supplément 2.6 : Différentielles et dérivées (4/4)

La vitesse d'écoulement, un exemple de vecteur

Le formalisme donné jusqu'à présent est valable non seulement pour les quantités scalaires telles que la température, mais aussi pour les vecteurs, par exemple le vecteur vitesse. En remplaçant dans l'équation

\frac{d T}{d t} = \frac{\partial T}{\partial t} + \vec{v} \cdot \nabla T

$T$ par $\vec{v}$ , on obtient :

\frac{d \vec{v}}{d t} = \frac{\partial \vec{v}}{\partial t} + (\vec{v} \cdot \nabla) \vec{v}

Les notations « forme lagrangienne et eulérienne » ainsi que « terme convectif » sont utilisées de la même manière. Il convient toutefois de prêter une attention particulière aux parenthèses. Qu'est-ce que cela signifie ?

Le terme $\vec{v} \cdot \nabla T$ dans l'exemple de la température est le produit scalaire des vecteurs $\vec{v}$ et $\nabla T$ . L'ordre de multiplication n'a pas d'importance dans ce cas : il est également correct de calculer d'abord $\vec{v} \cdot \nabla$ et de multiplier ensuite le résultat scalaire par $T$ .

Cependant, le terme $\nabla \vec{v}$ n'est pas défini, c'est pourquoi l'ordre de multiplication a son importance ici. Ceci est clarifié par les parenthèses dans le terme $(\vec{v} \cdot \nabla) \vec{v}$ . Le produit scalaire entre parenthèses devient

\vec{v} \cdot \nabla = u \frac{\partial}{\partial x} + v \frac{\partial}{\partial y} + w \frac{\partial}{\partial z}

et le résultat - un scalaire - est multiplié par $\vec{v}$ ,

(\vec{v} \cdot \nabla) \vec{v} = u \frac{\partial \vec{v}}{\partial x} + v \frac{\partial \vec{v}}{\partial y} + w \frac{\partial \vec{v}}{\partial z}

ses composantes cartésiennes :

\begin{array}{l} (\vec{v} \cdot \nabla) u = u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z} \\ (\vec{v} \cdot \nabla) v = u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z} \\ (\vec{v} \cdot \nabla) w = u \frac{\partial w}{\partial x} + v \frac{\partial w}{\partial y} + w \frac{\partial w}{\partial z} \end{array}

Tâche 5 : Opérateur Nabla et vecteur vitesse ↓

L'opérateur Nabla peut être lié à un vecteur, par exemple le vecteur vitesse.

a) Représentez les termes $\nabla \cdot \vec{v}$ et $\nabla \times \vec{v}$ ` en coordonnées cartésiennes. S'agit-il de scalaires ou de vecteurs ?

b) Quelle est la signification de ces termes ? Que signifie le terme $\vec{v} \cdot \nabla$ ?

Vous pouvez trouver les solutions sur ce site.

Par conséquent, la dérivée totale de la vitesse dans les composantes devient :

\frac{d u}{d t} = \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z}

\frac{dv}{d t} = \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z}

\frac{dw}{d t} = \frac{\partial w}{\partial t} + u \frac{\partial w}{\partial x} + v \frac{\partial w}{\partial y} + w \frac{\partial w}{\partial z}

Il s'agit des relations cinématiques fondamentales utilisées pour la description physique des courants : elles spécifient l'accélération de milieux déformables tels que l'air et l'eau.

En ajoutant d'autres termes d'accélération qui résultent des forces en tant que cause et effet de l'accélération, on obtient l'équation de la quantité de mouvement hydrodynamique. Si le frottement fait partie des forces, le résultat sera l'équation de Navier Stokes de l'hydrodynamique.

Mécanique des points de masse et des milieux déformables ↓

Si le « comment » du déroulement du mouvement d'un corps est représenté, on parle de cinématique du mouvement. Pour décrire le mouvement du point de masse d'un objet, qui est le centre de gravité, on utilise sa position $\vec{r} (t)$ , sa vitesse $\vec{v} (t) = \frac{d \vec{r} (t)}{d t}$ et son accélération $\vec{a} (t) = \frac{d \vec{v} (t)}{d t} = \frac{d^{2} \vec{r} (t)}{d t^{2}}$ .

Si l'on considère le « pourquoi » du mouvement, les forces qui influencent le mouvement entrent en jeu ; il s'agit de la dynamique du mouvement. L'équation du mouvement de Newton

\vec{F} = m \frac{d \vec{v}}{d t} = m \vec{a}

est un exemple pour un objet ayant une masse $m$ qui est accéléré par $\vec{a}$ sous l'effet d'une force extérieure $\vec{F}$ .

Pour les milieux déformables, c'est-à-dire les gaz et les liquides, le déplacement du centre de gravité aboutit rarement au résultat souhaité. En outre, les détails du mouvement de cet objet spatialement étendu et, dans la plupart des cas, structuré de manière complexe, y compris les processus internes, sont intéressants. L'équation du mouvement est formulée de manière analogue, en utilisant la masse par volume, c'est-à-dire la densité à l'endroit de la masse, $ρ = \frac{d m}{d V}$ , qui peut varier dans l'espace et le temps. De même, la densité de la force extérieure est introduite pour remplacer les forces extérieures :

\frac{d \vec{F}}{d V} = ρ \frac{d \vec{v}}{d t} = ρ \vec{a}

Un élément de masse infinitésimale est accéléré tout comme le centre de gravité d'un corps solide selon $\frac{d \vec{v}}{d t}$ . Dans ce cas, il s'agit de la sommation de l'accélération locale $\frac{\partial \vec{v}}{\partial t}$ et de l'influence des éléments environnants du milieu $(\vec{v} \cdot \nabla) \vec{v}$ , c'est-à-dire du terme convectif.

Equations ↓

Le graphique suivant montre les trajectoires des dériveurs de surface, avec une barre de couleur dans cet exemple, qui indique la vitesse de dérive en m/s. On constate que la vitesse de dérive est très variable et peut en outre prendre des valeurs élevées en haute mer. Il s'agit d'un exemple de représentation lagrangienne des courants.

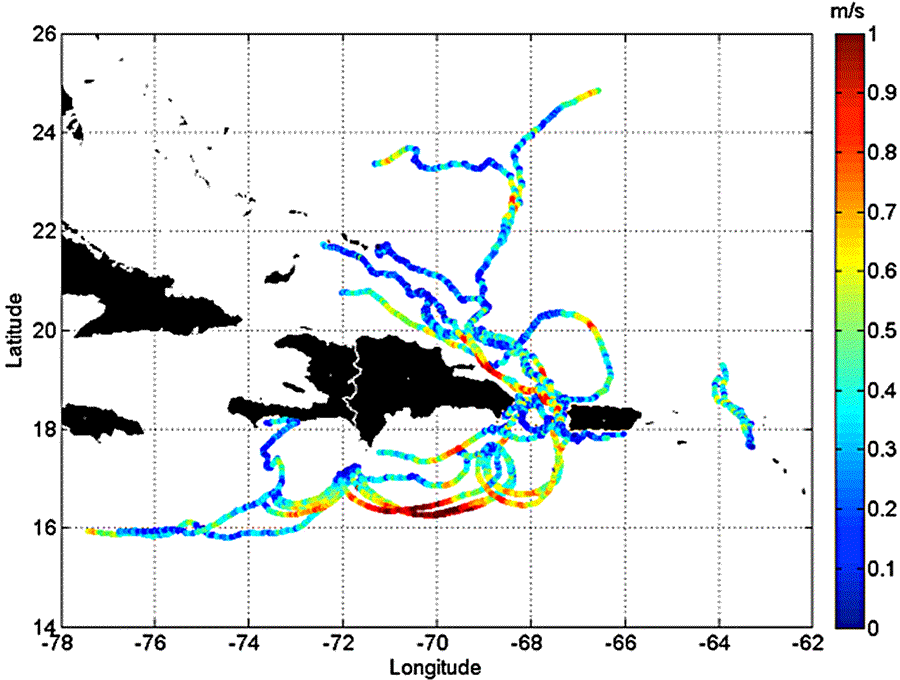
Drifting routes near the Dominican Republic and Puerto Rico

Trajectoires de 18 dériveurs de surface dans les environs de la République dominicaine et de Porto Rico. La barre de couleur indique la vitesse de dérive en m/s.
Source: Caribbean Coastal Ocean Observation System (Caribbean IOOS).

Le graphique suivant montre une série temporelle de courants océaniques sur deux jours dans la mer des Wadden de Basse-Saxe, près de l'île de Spiekeroog. Le diagramme montre la vitesse du courant, qui est caractérisée par le cycle d'une demi-journée des marées, et la direction du courant, qui est dominée par la direction nord-sud à travers l'entrée de la marée de Spiekeroog. Il s'agit d'un exemple de représentation eulérienne de la vitesse du courant.

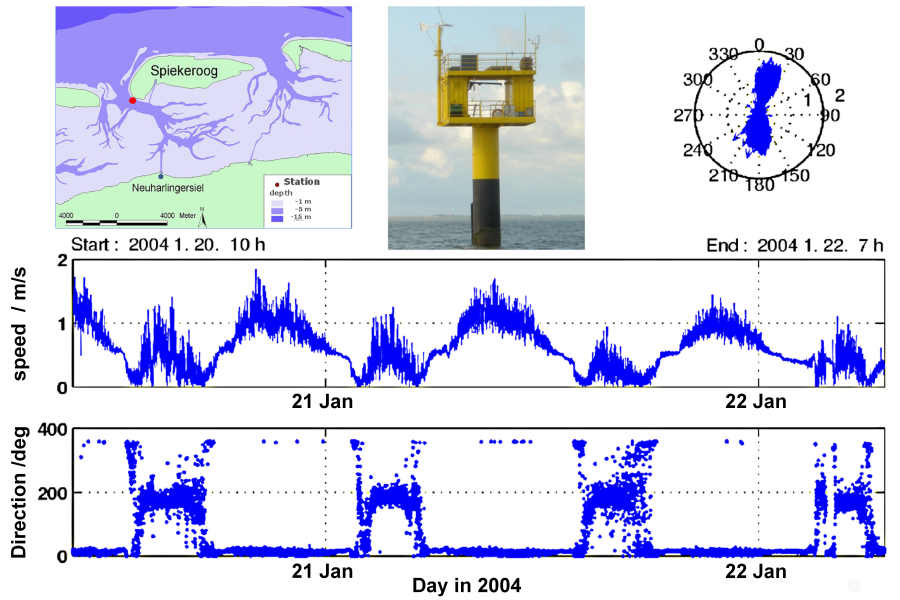
Courant dans le bras de mer de Spiekeroog

Données de courant prises à une station de séries temporelles dans le bras de mer de l'île de Spiekeroog. Au centre et en bas : quantité et direction du courant. En haut à droite : vecteurs de la vitesse du courant dans un diagramme de coordonnées polaires.

L'altimétrie radar par satellite permet de déterminer les courants océaniques globaux à partir de la topographie mesurée de la surface de l'océan. Pour cet aspect, vous pouvez trouver une vidéo réalisée il y a plusieurs années par le Scientific Visualization Studio de la NASA avec des liens supplémentaires comme exemple d'une représentation lagrangienne des courants océaniques.

Le spectre de la Terre

Supplément 2.6 : Différentielles et dérivées (4/4)

La vitesse d'écoulement, un exemple de vecteur