Supplément 4.3: Polarisation des ondes électromagnétiques, une introduction

La première approche

A la page 2 de la section sur les ondes électromagnétiques, nous avons développé des équations pour le champ électrique et le champ magnétique d'une onde plane monochromatique :

E (x, t) = E_{o} sin 2 π (\frac{x}{λ} - \frac{t}{T}) B (x, t) = B_{o} sin 2 π (\frac{x}{λ} - \frac{t}{T})

En raison du comportement périodique de la fonction sinus en $2 π$ , les équations montrent la périodicité avec la longueur d'onde λ et la période T. Au lieu de ces quantités, d'autres paramètres qui incluent le facteur $2 π$ sont utiles car les équations peuvent alors être écrites beaucoup plus brièvement. Ces paramètres sont les suivants :

le nombre d'ondes $k = \frac{2 π}{λ}$
la fréquence angulaire $ω = \frac{2 π}{T} = 2 π f$

Ce qui signifie que :

E (x, t) = E_{o} sin (k x - ω t) B (x, t) = B_{o} sin (k x - ω t)

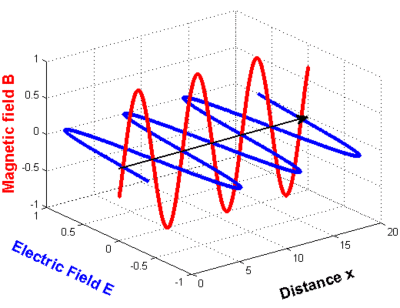
C'est ce à quoi ressemble l'onde dans un graphique :

Une onde électromagnétique se propageant de gauche à droite le long de l'axe x. Les courbes montrent les positions maximales des deux vecteurs de champ, qui sont perpendiculaires à l'axe x (flèche noire). Animation.

Les oscillations du champ électrique et du champ magnétique sont évidemment très régulières pour cette onde. Il s'agit d'une onde polarisée. Une onde est dite non polarisée si les oscillations sont complètement irrégulières. Les ondes peuvent être partiellement polarisées.
Seules les ondes transversales - par exemple les ondes électromagnétiques - peuvent être polarisées. Les ondes longitudinales - par exemple les ondes sonores - ne sont pas polarisées.

Dans les graphiques ci-dessus, rien n'est dit sur la direction du champ électrique et du champ magnétique (si ce n'est qu'ils sont perpendiculaires l'un à l'autre et à la direction de propagation) : les coordonnées y et z manquent pour représenter la direction des vecteurs d'intensité du champ.

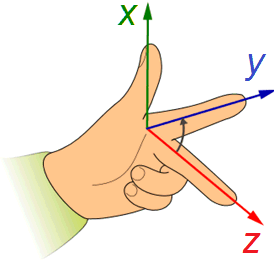
Nous examinons maintenant une onde qui se propage dans la direction x dans un système de coordonnées tridimensionnelles droites $(x, y, z)$ . Seul le champ électrique est examiné ; les résultats sont également valables pour le champ magnétique oscillant orthogonalement.

Coordonnées cartésiennes gauche et droite.

Le vecteur de champ $\vec{E}$ est orthogonal à la direction de propagation x. Il est divisé en composantes le long des directions y et z:

E_{y} = E_{y, o} sin (k x - ω t) E_{z} = E_{z, o} sin (k x - ω t + φ)

$E_{y, o}$ et $E_{z, o}$ sont les amplitudes. La quantité $φ$ indique le déphasage entre les deux composantes. Pour une onde monochromatique, $φ$ est constante, les deux composantes de l'onde sont donc cohérentes.

Les valeurs de

E_{y, o}

E_{z, o}

φ

caractérisent complètement le type de polarisation d'une onde monochromatique : Elle peut être linéaire, circulaire ou elliptique.

Les principaux types de polarisation et leurs caractéristiques d'oscillation, $n$ étant un nombre entier :

Condition	Type de polarisation
$E_{z, o} = 0$	linéaire le long de l'axe y
$E_{y, o} = 0$	linéaire le long de l'axe z
$φ = 2 n π$ $E_{y} = \frac{E_{y, o}}{E_{z, o}} E_{z}$	linéaire en diagonale dans les premier et troisième quadrants du plan y,z
$φ = (2 n + 1) π$ $E_{y} = - \frac{E_{y, o}}{E_{z, o}} E_{z}$	linéaire en diagonale dans les deuxième et quatrième quadrants du plan y,z
$φ = (2 n - \frac{1}{2}) π$ $E_{y, o} = E_{z, o}$	circulaire droite : Les vecteurs de champ tournent à droite (face à la vague). *Animation* des têtes de vecteurs tournantes, le champ E est représenté en bleu, le champ B en rouge.
$φ = (2 n + \frac{1}{2}) π$ $E_{y, o} = E_{z, o}$	circulaire gauche : Le vecteur de champ tourne à gauche (face à la vague)
$φ = (2 n - \frac{1}{2}) π$ $E_{y, o} \neq E_{z, o}$	elliptique droite : Les vecteurs de champ tournent à droite (face à l'onde). *Animation* des têtes de vecteurs tournantes, le champ E est représenté en bleu, le champ B en rouge.
$φ = φ (t)$ $E_{y, o} = E_{z, o}$	lumière naturelle non polarisée

La lumière naturelle n'est pas monochromatique mais présente une large gamme spectrale, $φ$ change de façon statistiquement permanente. Les composantes y et z ne sont pas cohérentes entre elles.

La lumière partiellement polarisée est composée de lumière polarisée et non polarisée. Elle est caractérisée par le degré de polarisation :

p = (Intensité de la partie polarisée)/(Intensité totale)

Pour caractériser la lumière partiellement polarisée, quatre quantités sont nécessaires : Les valeurs de