Supplement 4.8: Een experiment met de lichtverstrooiing van water

Lichtverstrooiing door water, een voorbeeld van Rayleigh-verstrooiing

De absorptiecoëfficiënt van vloeibaar water... is minder dan 1/m voor alle zichtbare golflengten. In het blauwe bereik is water bijzonder transparant, daar is de absorptiecoëfficiënt ongeveer 0,02/m.

De verstrooiingscoëfficiënt van water is ongeveer een factor 10 kleiner in het blauwe gebied. Dit komt door de geringe grootte van het molecuul in vergelijking met de golflengte van het licht: de diameter is ongeveer 2 Å of 2·10^-10 m (de Ångström, met het eenheidsteken Å, is een gangbare lengte-eenheid in de atoomfysica). Watermoleculen zijn dus een voorbeeld van deeltjes die worden gekenmerkt door Rayleigh-verstrooiing.

Hier onderzoeken we hoe een watermonster het licht van een laser verstrooit.

De experimentele opzet

Een met water gevulde cuvet wordt verlicht met een blauwgroene laserstraal. De golflengte is 500 nm, het stralingsvermogen is 1 W (als u het experimenteel wilt nabootsen: deze laser is absoluut niet oogveilig, wees uiterst voorzichtig).

Onder een hoek van 90° tegen de richting van de laserstraal in, nemen we eerst met het oog het verstrooide licht waar dat op het water wordt geproduceerd. Laat het verlichte en zichtbare watervolume V = 1 cm³ bedragen.

Experimentele opstelling voor de meting van de lichtverstrooiing van een watermonster.
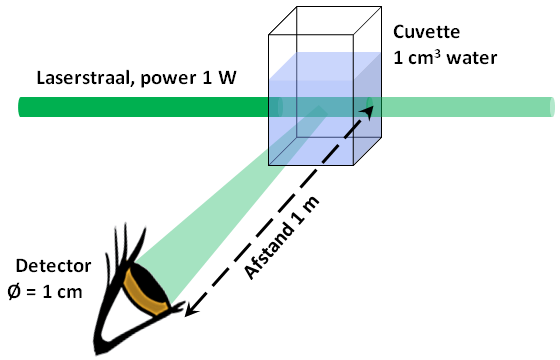
Bron: Rainer Reuter, Universiteit van Oldenburg, Duitsland.

Vervolgens bevestigen we een fotodiode voor een kwantitatieve meting op een afstand van r = 1 m van de cuvette en ook onder een hoek van 90°. Laat de diameter van het lichtgevoelige gedeelte d = 1 cm. zijn. Laat de gevoeligheid van de fotodiode bij 500 nm, d.w.z. de fotostroom (in ampère) van de diode bij een optisch vermogen (in watt), gelijk zijn aan S = 0,5 A/W.

Verstrooiingseigenschappen van water

Zeer kleine deeltjes verstrooien het licht symmetrisch in de voorste en achterste helft van de ruimte, dit is kenmerkend voor de Rayleigh-verstrooiing van kleine deeltjes. Als de verstrooiingshoek gemeten ten opzichte van de richting van de laserstraal straal wordt aangeduid met θ, wordt de verstrooiingsfunctie voor ongepolariseerd licht gegeven door de vergelijking

β (θ) = β (90 °) (1 + {cos}^{2} θ)

Polair diagram van de fasefunctie versus hoek θ voor deeltjes met de diameter 2 Å, met de brekingsindex n = 1,33 en voor licht met golflengte 500 nm. De fasefunctie is gelijk aan de verstrooiingsfunctie β gedeeld door de verstrooiingscoëfficiënt b.
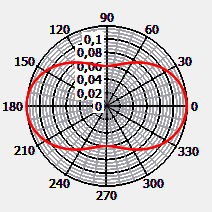
Gemaakt met MieSimulatorGUI, versie 1.3, laatste toegang: 30 Maart 2023.

De literatuurwaarde van de verstrooiingsfunctie voor de verstrooiingshoek 90° bij de golflengte 500 nm is (Zhang & Hu, 2021):

β (90 °) = 1,38 \cdot 10^{- 4} \frac{1}{m sr}

Vergelijkingen ↓

De molaire massa van water is ongeveer 18 g, overeenkomstig is het molaire volume ongeveer 18 cm³. Het aantal deeltjes in de mol wordt gegeven door de Avogadro-constante 6·10²³. Het aantal watermoleculen in 1 m³ is dan:

N = \frac{6 \cdot 10^{23}}{18 \cdot 10^{- 6} m^{3}} = 3,3 \cdot 10^{28} \frac{1}{m^{3}}

De differentiële doorsnede van de verstrooiing bij 90° resulteert in:

σ (90 °) = \frac{β (90 °)}{N} = 4,14 \cdot 10^{- 33} \frac{m^{2}}{sr}

De helderheid op het oog

De intensiteit van het verstrooide licht volgt uit de waarden van de verstrooiingsfunctie β van het water en de bestralingssterkte E van de laser op het verlichte watervolume V volgens

I = β E V

waarbij E = 1 W/cm² en V = 1 cm³. Het optisch vermogen bij het oog of de detector is het resultaat van deze intensiteit vermenigvuldigd met de ruimtehoek Ω waarbij het oog of de detector gezien vanuit het verstrooiende water verschijnt:

P = I (90 °) Ω = β (90 °) E V \frac{π d^{2} / 4}{r^{2}}

Als je alle waarden substitueert, krijg je het optisch vermogen P ≈ 10^-10 W of 0,1 nanowatt. Kan het oog dit nog zien?

Om dit te beoordelen, is het nuttig om over te gaan naar het fotonbeeld van licht. Een aan het donker aangepast oog kan ongeveer elk 50e foton dat op het netvlies valt, waarnemen als een zwakke lichtflits. Voor monochromatisch licht is de relatie tussen optisch vermogen en het corresponderende aantal fotonen als volgt:

P = N_{P h o t o n} E_{P h o t o n}

waarbij N_Photon het aantal fotonen per seconde is en de fotonenergie E_Photon = hc/λ. h is de constante van Planck en c is de lichtsnelheid. Hieruit volgt N_Photon ≈ 250· 10⁶ of 250 miljoen fotonen per seconde..

Het signaal van de detector

De fotostroom van de fotodiode is het resultaat van het invallend optisch vermogen en van zijn gevoeligheid, waarvan hierboven is aangenomen dat die S = 0,5 A/W is. Dit wordt:

I_{p h o t o} = S P = 0,5 \cdot 10^{- 10} A

of 50 picoampère. Elektrische multimeters reiken in het beste geval maar tot in het microampèrebereik, dus heb je een veel gevoeligere ampèremeter nodig. Zulke apparaten worden picoampèremeters genoemd.

De verstrooiingscoëfficiënt

Als de verstrooiingsfunctie geïntegreerd wordt over de hele ruimte, resulteert dit in de verstrooiingscoëfficiënt:

\begin{array}{l} b = \int_{Ω = 4 π} β d Ω = 2 π \int_{θ = 0}^{π} β (θ) sin θ d θ \\ = 2 π β (90 °) \int_{θ = 0}^{π} (1 + {cos}^{2} θ) sin θ d θ = 16 \frac{π}{3} β (90 °) \end{array}

Invoegen geeft: $b = 2,3 \cdot 10^{- 3} /m$

Over een afstand van 1 m verliest de laserstraal 2,3 promille van zijn helderheid door verstrooiing. De totale doorsnede van de verstrooiingsdoorsnede (geïntegreerd over de hele ruimte) wordt:

σ = \frac{b}{N} = 7 \cdot 10^{- 32} m^{2}

In vergelijking met hun geometrische dwarsdoorsnede overschaduwen de moleculen dus slechts een zeer klein deel van de helderheid van de laserstraal.

In feite zijn er nog enkele andere variabelen die de lichtverstrooiing van water beïnvloeden. Temperatuur, druk en - in het geval van zeewater - zoutgehalte spelen een rol. En er treden dichtheidsfluctuaties op in de vloeistof, die ook bijdragen aan de verstrooiing. De publicatie van Zhang & Hu, 2021 geeft hierover gedetailleerde informatie.