5. Oefeningen

2. Thermische straling

Supplement 2.1: Absorptie, emissie en reflectie

Taak: Van onbalans naar evenwicht

Twee lichamen in een thermisch evenwicht in een geïsoleerde holte. De pijlen stellen elk verschillende stralingsfluxen voor. De letters g, u en o op de korte pijlen staan voor gereflecteerd, uitgestraald en geabsorbeerd.

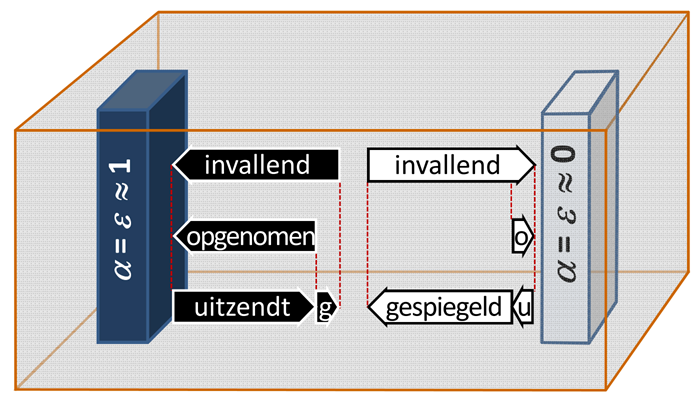
Schets zoals weergegeven in de grafiek in hoeverre de lengte van de flitsen zou veranderen in de volgende gevallen:

het zwarte lichaam heeft een hogere temperatuur dan het witte lichaam
het witte lichaam heeft een hogere temperatuur dan het zwarte lichaam.

Vragen:

hoe verandert de lengte van de pijlen voor de geabsorbeerde en de uitgezonden straling van beide lichamen?
welke lengte van de pijlen resulteert voor de inkomende zoals de gereflecteerde straling?
herken hoe de neiging tot benadering van de temperaturen kan ontstaan.

Antwoord:

De situatie is vrij complex en op het eerste gezicht verwarrend. Schetsen van stralingsbalansen zijn erg nuttig voor een goed begrip. Hieronder worden enkele nuttige tips gegeven. Ze zijn gericht op de beginvoorwaarden van twee lichamen die met elkaar in contact komen, waarbij het ene lichaam een hogere temperatuur heeft en het andere de temperatuur van het aanvankelijke evenwicht.

a) Het zwarte lichaam heeft een hogere temperatuur dan het witte.

1: Zwart lichaam: uitgezonden en geabsorbeerd zijn sterker. Wit lichaam: uitgezonden blijft hetzelfde, geabsorbeerd is sterker.
2: Zwart lichaam: invallend en gereflecteerd zijn sterker. Wit lichaam: invallend en gereflecteerd zijn sterker.
3: De emissie van het witte lichaam blijft gelijk, alle andere grootheden nemen toe; de balans voor het witte lichaam is sterker dan voor het zwarte lichaam.

b) Het witte lichaam heeft een hogere temperatuur dan het zwarte.

1: Zwart lichaam: uitgezonden blijft gelijk, geabsorbeerd is sterker. Wit lichaam: uitgezonden en geabsorbeerd zijn sterker.
2: Zwart lichaam: invallend en gereflecteerd zijn sterker. Wit lichaam: invallend en gereflecteerd zijn sterker.
3: De emissie van het witte lichaam blijft gelijk, alle andere grootheden nemen toe; de balans voor het zwarte lichaam is sterker dan voor het witte lichaam

Supplement 2.6: Differentialen en afgeleiden

Opdracht 1: partiële afgeleiden en differentialen

Bereken de partiëële afgeleiden en de totale differentiaal van de volgende functies:

z = x^{3} y + x^{2} y^{2} + x y^{3}

z = x sin y - y sin x

Antwoorden:

z = x^{3} y + x^{2} y^{2} + x y^{3}

De partiëële afgeleiden:

\frac{\partial z}{\partial x} = 3 x^{2} y + 2 x y^{2} + y^{3}

\frac{\partial z}{\partial y} = x^{3} + 2 x^{2} y + 3 x y^{2}

Het differentiaal:

d z = (3 x^{2} y + 2 x y^{2} + y^{3}) d x + (x^{3} + 2 x^{2} y + 3 x y^{2}) d y

z = x sin y - y sin x

De partiëële afgeleiden:

\frac{\partial z}{\partial x} = sin y - y cos x

\frac{\partial z}{\partial y} = x cos y - sin x

Het differentiaal:

d z = (sin y - y cos x) d x + (x cos y - sin x) d y

Opdracht 2: totale afgeleiden

Bereken de totale afgeleide van

z = x^{2} + 3 x y + 5 y^{2}

waarbij $x = sin t$ en $y = cos t$ .

Antwoord:

De partiëële afgeleiden:

\frac{\partial z}{\partial x} = 2 x + 3 y

\frac{\partial z}{\partial y} = 3 x + 10 y

Afgeleiden van de variabelen:

\frac{d x}{d t} = cos t

\frac{d y}{d t} = - sin t

Het totale differentieel:

\frac{d z}{d t} = (2 sin t + 3 cos t) cos t - (3 sin t + 10 cos t) sin t

Opdracht 3: Partiële afgeleide en totale differentiaal van een vector

De rekenregel voor de differentiaal geldt niet alleen voor scalaire functies, maar op dezelfde manier ook voor vectoren. We beschouwen de vector $\vec{A} (x, y, z)$ :

d \vec{A} = \frac{\partial \vec{A}}{\partial x} d x + \frac{\partial \vec{A}}{\partial y} d y + \frac{\partial \vec{A}}{\partial z} d z

Bereken de partiële afgeleiden en de totale differentiaal van

\vec{A} = (x^{2} sin y, z^{2} cos y, - x y^{2})

Oplossing:

Gebaseerd op de definitie van het totale verschil:

\begin{array}{l} d \vec{A} = \frac{\partial \vec{A}}{\partial x} d x + \frac{\partial \vec{A}}{\partial y} d y + \frac{\partial \vec{A}}{\partial z} d z \\ = (2 x sin y,0, - y^{2}) d x + (x^{2} cos y, - z^{2} sin y, - 2 x y) d y \\ + (0,2 z cos y,0) d z \\ = (2 x sin y d x + x^{2} cos y d y, - z^{2} sin y d y 2 z cos y d z, - y^{2} d x - 2 x y d y) \end{array}

Je kunt ook het totale verschil van elke afzonderlijke term van $\vec{A}$ direct berekenen:

\begin{matrix} d \vec{A} = (d (x^{2} sin y), d (z^{2} cos y), d (- x y^{2})) \\ = (2 x sin y d x + x^{2} cos y d y, - z^{2} sin y d y 2 z cos y d z, - y^{2} d x - 2 x y d y) \end{matrix}

Opdracht 4: Temperatuur in ruimte en tijd

De temperatuur kan worden gegeven door de functie

T = T_{o} + a x - b x y^{2} + c y z^{2} + d z t

met:
$T_{o}$ =20°C
$a$ =0,3°C/m
$b$ =0,02°C/m³
$c$ =0,1°C/m³
$d$ =0,01°C/(m·s)

a) Wat is de temperatuur op de locatie $\vec{r}' = (x', y', z')$ = (10 m, 5 m, 2 m) op het tijdstip $t'$ = 100 s.

b) Bereken de partiëële afgeleiden van de temperatuur. Welke waarden verkrijg je voor de locatie $\vec{r}'$ en op het tijdstip $t'$ ?

c) Bereken het temperatuurverschil $d T$ voor de verplaatsing
$d \vec{r} = (d x, d y, d z)$ = (1 m, 0.5 m, 0.5 m) met de tijd $d t$ = 2 s later.
(We behandelen de differentialen voor de benadering als eindige grootheden)

d) Welke waarden heeft de temperatuur $T (\vec{r}' + d \vec{r}, t' + d t)$ ?

Antwoorden:

a) $T (\vec{r}')$ = 22°C

b)	$\frac{\partial T}{\partial x} = a - b y$	${(\frac{\partial T}{\partial x})}_{\vec{r}', t'}$ = 0,2°C/m
	$\frac{\partial T}{\partial y} = - 2 b x y + c z^{2}$	${(\frac{\partial T}{\partial y})}_{\vec{r}', t'}$ = 0,4°C/m
	$\frac{\partial T}{\partial z} = 2 c y z + d t$	${(\frac{\partial T}{\partial z})}_{\vec{r}', t'}$ = 3°C/m
	$\frac{\partial T}{\partial t} = d z$	${(\frac{\partial T}{\partial t})}_{\vec{r}', t'}$ = 0,02°C/m

c) $d T$ = 1,94°C

d) $T (\vec{r}' + d \vec{r}, t' + d t)$ = 21,94°C

Opdracht 5: Nabla-operator en snelheidsvector

De Nabla-operator kan gekoppeld worden aan een vector, bijvoorbeeld de snelheidsvector.

a) Geef de termen weer $\nabla \cdot \vec{v}$ en $\nabla \times \vec{v}$ ` in cartesische coördinaten. Zijn het scalaren of vectoren?

b) Wat is de betekenis van deze termen? Wat betekent de term $\vec{v} \cdot \nabla$ ?

Antwoorden:

\nabla \cdot \vec{v} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z}

\nabla \times \vec{v} = | \begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ u & v & w \end{matrix} | = ((\frac{\partial w}{\partial y} - \frac{\partial v}{\partial z}), (\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x}), (\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}))

met de eenheidsvectoren $\vec{i}$ , $\vec{j}$ en $\vec{k}$ in richtingen van de coördinaatassen $x$ , $y$ en $z$ .

$\nabla \cdot \vec{v}$ is een scalair, $\nabla \times \vec{v}$ is een vector.

De term $\nabla \cdot \vec{v}$ wordt ook wel de divergentie van de snelheid genoemd en verwijst naar bronnen of putten van snelheid. Een positieve balans duidt op een bron van snelheid in de regio, zoals bijvoorbeeld bij een uitdijend gas. Een negatieve balans geeft een compressie van een gas weer. Trefwoord voor verder lezen: Stelling van Gauss.

De term $\nabla \times \vec{v}$ wordt ook wel de rotatie van de snelheid genoemd en verwijst naar de vorticiteit. Deze is niet nul in de aanwezigheid van schuifstromingen, wervelingen en turbulenties. Trefwoord voor verder lezen: Stokes' stelling.

$\vec{v} \cdot \nabla$ is de vermenigvuldiging van de snelheidsvector en de Nabla-operator. De differentiaaloperator moet worden toegepast op een andere grootheid, een scalair of een vector. Zie Supplement 2.6, page 3.