2. Mit Zeitreihen arbeiten

Lineare Regressionsanalyse (2/3)

Schritt 2: Die Steigung (Fortsetzung)

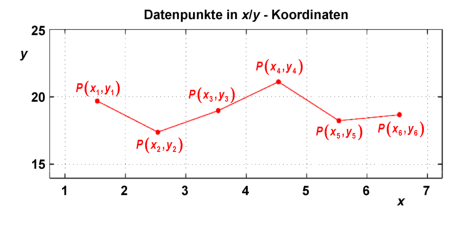
Wir untersuchen die Julitemperaturen, konvertiert zu Punkten $P (x_{i}, y_{i})$ mit i=1, ..., 6, wie in der Datentabelle angegeben.

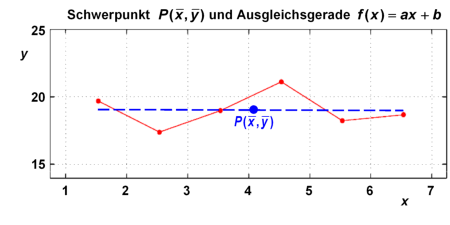
Wir haben schon den Schwerpunkt $P (\bar{x}, \bar{y})$ der Daten berechnet, er liegt bei $\bar{x} = 4,08$ und $\bar{y} = 19,01$ .

Die Steigung a der Ausgleichsgeraden

f (x) = a x + b

zu der die Datenpunkte den kleinsten Abstand haben, berechnet sich nach der sogenannten Methode der kleinsten Quandrate zu:

a = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}

Eine Ableitung der Gleichung findet sich wieder in Ergänzung 1. Mit den Temperaturdaten folgt:

a = \frac{(x_{1} - \bar{x}) (y_{1} - \bar{y}) + ... + (x_{6} - \bar{x}) (y_{6} - \bar{y})}{{(x_{1} - \bar{x})}^{2} + ... + {(x_{6} - \bar{x})}^{2}} = - 0,0117

Mit der Punkt-Steigungs-Form wird die Ausgleichsgerade nun:

f (x) - \bar{y} = a (x - \bar{x})

Schritt 3: Der Schnittpunkt mit der y-Achse

Der Schnittpunkt b der Ausgleichsgerade lässt sich berechnen, wenn man die oben angegebene Gleichung umschreibt:

b = \bar{y} - a \bar{x} = 19,01

Damit wird schließlich:

f (x) = - 0,0117 x + 19,01

Datenpunkte, ihr Schwerpunkt

P (\bar{x}, \bar{y})

und die Ausgleichsgerade

f (x) = a x + b

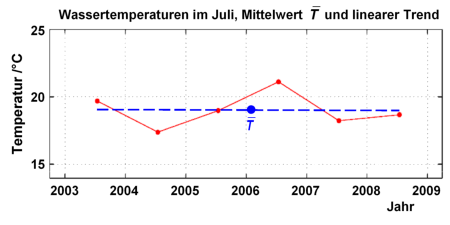
Überführt man dies wieder in die Meerwassertemperaturen im Juli, so folgt:

T (t) = - 0,0117 t + 42,50

mit der Temperatur T in °C und dem Kalenderjahr t.

Meerwassertemperaturen bei Spiekeroog im Juli 2003-2008, mittlere Temperatur in diesen Jahren und linearer Temperaturtrend.