Ergänzung 2.1: Punktwolken und Ausgleichsgeraden (3/3)

Der Korrelationskoeffizient

Wir untersuchen eine Punktwolke $P(x_i,y_i)$, mit i=1, ..., n. Die Punkte sind durch einen Satz von n Merkmalspaaren $x_i$ und $y_i$ definiert. Wie bereits gezeigt, kann der Schwerpunkt der Punktwolke und die Ausgleichsgerade bestimmt werden. Wir interessieren uns für eine Größe, die angibt, wie sehr die Punkte von der Ausgleichsgerade abweichen. Hierzu betrachten wir als Beispiel den Punkt $P(x_5,y_5)$ in der unten dargestellten Grafik, und seine durch die Ausgleichsgerade vorhergesagte Position $P\left(x_5,f(x_5)\right)$.

Wassertemperaturen im Oktober bei Spiekeroog (blaue Datenpunkte), Ausgleichsgerade (rote durchbrochene Linie) und Schwerpunkt $P(\overline{x},\overline{y})$. Der Datenpunkt $P(x_5,y_5)$ ist verglichen mit seinem durch die Ausgleichsgerade vorhergesagten Wert $P\left(x_5,f(x_5)\right)$.

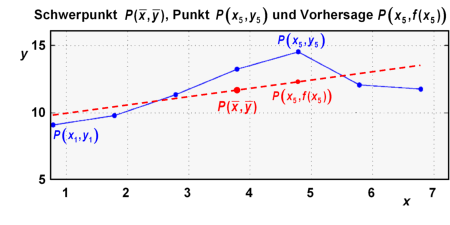
Die Lage von $P(x_5,y_5)$ wird, wie im unten dargestellten Diagramm dargestellt, in zwei Schritten erklärt:

• die Lage des durch die Ausgleichsgerade vorhergesagten Punktes $P\left(x_5,f(x_5)\right)$ bei gleichem x=x₅:  $f(x_5)-\overline{y}$
  (durch die Ausgleichsgerade vorhergesagte Abweichung)
• die Abweichung von $P(x_5,y_5)$ zu $P\left(x_5,f(x_5)\right)$: $y_5-f(x_5)$
  (unerklärte Abweichung)

Erklärung der Lage von $P(x_5,y_5)$ in zwei Schritten: durch die Ausgleichsgerade vorhergesagter Teil (untere Klammer) und unerklärter Teil (obere Klammer).

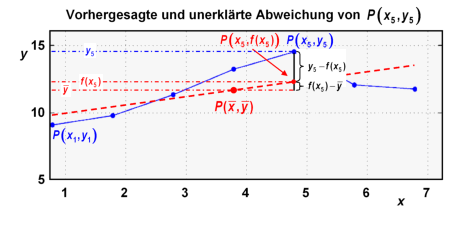
Dieses Konzept kann auf alle Punkte der Punktwolke übertragen werden, um ihre Abweichung von der Ausgleichsgeraden darzustellen.

Der lineare Korrelationskoeffizient

Die in Kapitel 2 auf der Seite Lineare Regressionsanalyse (3/3) genutzte Gleichung für den Korrelationskoeffizienten unterscheidet sich von der Beziehung in der linken Spalte. Sie gilt ausschließlich für Ausgleichsgeraden (daher: linearer Korrelationskoeffizient), während die Gleichung links auch für gekrümmte Ausgleichsfunktionen richtig ist.

Die Gleichung für den linearen Korrelationskoeffizienten erhält man durch Quadrieren der Gleichung in der linken Spalte und Ersetzen von $f(x_i)-\overline{y}$ durch $a(x_i-\overline{x})$:

Mit der auf der vorherigen Seite angegebenen Steigung a folgt:

Durch Kürzen vereinfacht sich dies zu:

Ziehen der Wurzel ergibt schließlich:

Lässt man die Betragsstriche weg,

so kann der linearer Korrelationskoeffizient auch negative Werte einnehmen: man gibt üblicherweise r das gleiche Vorzeichen wie a.

Vorteilhaft an der Gleichung ist, dass ausschließlich die Koordinaten des Schwerpunkts und der Datenpunkte eingehen, die Gleichung in der linken Spalte erfordert auch Koordinatenwerte der Ausgleichsfunktion.