2. Mit Zeitreihen arbeiten

Lineare Regressionsanalyse (3/3)

Schritt 4: Der Korrelationskoeffizient

Wir betrachten eine Anzahl Datenpunkte P( x i , y i ) mit i=1, ..., n, ihren Schwerpunkt P( x ¯ , y ¯ ) , und die mit der linearen Regressionsanalyse berechnete Ausgleichsgerade f(x)=ax+b . Es ist oft wichtig, die Qualität der Ausgleichsgeraden zu wissen. Dies bedeutet: wie gut werden die Daten durch diese Gerade beschrieben? Sie wäre eine ideale Darstellung der Daten, wenn alle Datenpunkte exakt auf ihr lägen. Bei ‘echten’ Daten ist das nicht so, es gibt Abweichungen.

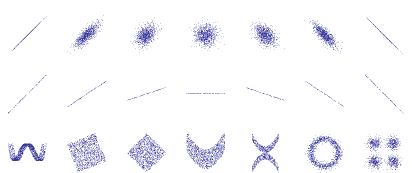
Der Korrelationskoeffizient r ist eine Größe, mit er sich die Abweichungen der Daten von ihrer Ausgleichsgerade angeben lassen. Er liegt zwischen -1 und +1, wobei r=+1 oder -1 einer idealen Korrelation (also einer idealen Übereinstimmung der Daten mit der Ausgleichsgerade) und r=0 einem Fehlen jeglicher Korrelation (die Daten lassen sich nicht durch eine Gerade darstellen) entspricht. Das Vorzeichen von r ist das gleiche wie das Vorzeichen der Steigung a der Ausgleichsgeraden: a>0 ergibt positive r, a<0 negative r.

Der Korrelationskoeffizient wird mit der folgenden Gleichung berechnet:

r= ∑ i=1 n ( x i − x ¯ )( y i − y ¯ ) ∑ i=1 n ( x i − x ¯ ) 2    ∑ i=1 n ( y i − y ¯ ) 2

Mit den Daten der Meerwassertemperatur im Juli ...

Jahr xi yi
2003 1,58 19,69
2004 2,58 17,38
2005 3,58 18,98
2006 4,58 21,12
2007 5,58 18,23
2008 6,58 18,67

... findet man:                    r=−0,017

Dieses Ergebnis liegt sehr nahe bei Null. Was bedeutet das? Die berechnete Steigung a der Ausgleichsgeraden ist ebenfalls nahe Null, die Ausgleichsgerade verläuft fast waagerecht. Damit liegt im Ergebnis der Regressionsanalyse praktisch kein Trend der Daten in Richtung veränderlicher y-Werte (oder: Temperaturen) mit zunehmendem x (oder: Kalenderjahren) vor. Also hängen die y-Werte der Daten von x gar nicht ab, sie sind unkorreliert!



Frage: Korreliert oder unkorreliert? ↓


Manche Ergebnisse der Regressionsanalyse sind so nicht zu erwarten gewesen:
  • Oft kann man eine Ausgleichsgerade leicht von Hand zeichnen. Aber das Beispiel der Sommertemperaturen an der Nordseeküste zeigt, dass man die Größe eines eventuellen Temperaturtrends nicht immer durch Betrachtung der Daten abschätzen kann: hier war die Steigung der Ausgleichsgeraden nur schwer zu schätzen
  • Die Berechnung mit der linearen Regressionsanalyse ist recht einfach durchzuführen. Mit nicht allzu vielen Daten kann man dies mit einem Taschenrechner tun.
  • In unserem Beispiel war über die Jahre 2003 bis 2008 ein eindeutiger Trend der Meerwassertemperatur nicht feststellbar: die Steigung der Ausgleichsgerade ist praktisch Null. In solchen Fällen hängen die beiden betrachteten Merkmale Temperatur und Zeit nicht voneinander ab: sie sind nicht korreliert.


Weiterführende SEOS-Seiten