Temperaturtrend im Wattenmeer 2:
Lineare Regressionsanalyse

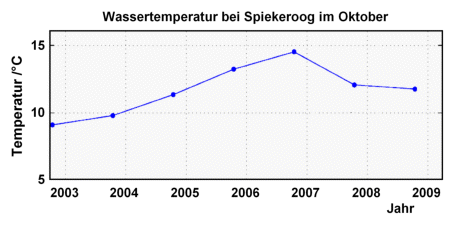
Szenario

Beim Surfen im Internet fand ich Messreihen über die Luft- und Wassertemperatur und sogar über den Salzgehalt des Meerwassers an der Nordseeküste bei Spiekeroog. Rechts sehen wir diese Grafik mit allen Messwerten, die über die Jahre gemessen worden sind.

Ich fand aber auch Mittelwerte für jeden Monat. Die Mittelwerte habe ich heruntergeladen und hier abgelegt. Sie beginnen im Oktober 2002 und reichen bis März 2009. Die Spalten enthalten jeweils das Jahr, den Monat im Jahr, die Luft- und Wassertemperatur und den Salzgehalt des Meerwassers, immer bei Spiekeroog gemessen. Können wir mit diesen Daten zeigen, dass es an der Nordsee immer wärmer wird, wie es in den Zeitungen steht? Das müssen wir uns genauer ansehen.

Gibt es einen Trend zu höheren Temperaturen, dann müsste man das sehen, wenn man die Monatsmittelwerte von Oktober 2002 bis März 2009 über die Monate in eine Grafik einträgt. Der Trend sollte dann eine ansteigende Kurve ergeben. Wächst die Temperatur proportional zur Zeit, dann ist die Kurve eine ansteigende Gerade.

Kürzlich stand in der Zeitung, dass vor allem die Temperaturen im Herbst in den letzten Jahren stark zugenommen haben. Also habe ich die Wassertemperaturen im Oktober in ein Diagramm gezeichnet. Das Ergebnis sieht man hier:

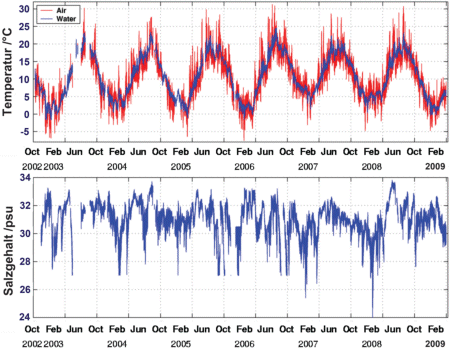
Zeitreihe der Temperatur der Luft (rote Kurve), des Wassers (blaue Kurve) und des Salzgehalts von Oktober 2002 bis März 2009. Salzgehalte sind in psu angegeben, was der Menge Salz in Gramm pro Kilogramm Meerwasser entspricht. Die Markierungen an der Zeitachse entsprechen jeweils dem 1. April und 1. Oktober.

Gar nicht so einfach... Bis 2006 steigt die Temperatur kräftig an, aber dann geht sie wieder zurück. ;-(

Wie kann man die “richtige” Gerade finden, die den Trend am besten wiedergibt? Sie müsste so im Diagramm liegen, dass der Abstand aller Datenpunkte - also die Abweichung aller tatsächlich gemessenen Werte - kleiner als bei allen anderen Geraden ist, die man ebenfalls einzeichnen könnte! Das Verfahren, mit dem man diese Gerade bestimmt, heißt lineare Regression nach der Methode der kleinsten Quadrate,, und die so gefundene Gerade ist die Ausgleichsgerade.

Ausgleichsgeraden

Die Frage nach einem Temperaturtrend an der Nordsee zeichnet sich durch zwei Merkmale aus, die Temperatur und die Zeit. Das ist nicht bei allen Problemen der Fall. Die Ergebnisse eines Würfelspiels weisen nur ein Merkmal auf: die gewürfelte Zahl. In vielen Fällen gibt hängt ein Merkmal vom anderen ab. Eine Schraubenfeder wird sich umso mehr ausdehnen (ein Merkmal), je größer das Gewicht ist (das andere Merkmal), das man an ihr aufhängt. Die Auslenkung ist dem Gewicht proportional; dies ist das Hookesche Gesetz, das Sie in der Mechanik vermutlich kennengelernt haben. Linearität ist ein anderes Wort für Proportionalität. Ein linearer Zusammenhang von Merkmalen gilt aber meist nur in Grenzen: überdehnt man die Feder, dann ermüdet sie und verhält sich nichtlinear.

Die Auslenkung der Feder und das an ihr angebrachte Gewicht hängen zusammen, sie sind miteinander korreliert. Es gibt ebenfalls einen Zusammenhang zwischen dem Anstieg der Temperaturen auf der Erde und der in den vergangenen 100 Jahren verstrichenen Zeit: die Korrelation wird durch das zeitliche Anwachsen der Treibhausgase in der Atmosphäre erzeugt.

Oft ist es jedoch ein Zufall und nicht kausal bedingt, wenn solche Merkmale voneinander abzuhängen scheinen. Beispiel: eine Zeitung berichtet, die Abnahme der Störche auf dem Land geht mit einer abnehmenden Geburtenstatistik einher. Korreliert oder nicht?

Eigentlich spricht nichts dafür, dass die Temperatur im Watt linear mit der Zeit wächst. Betrachtet man einen Zeitraum von 100 Jahren, dann trifft dies vermutlich nicht zu. Eine gekrümmte Kurve kann aber in kleinen Bereichen meist recht gut durch eine Gerade (eine Tangente an die gekrümmte Kurve) angenähert werden. Dies vermuten wir auch für die Temperatur, wenn man sie nur über einige Jahre betrachtet. Dann kann man eine Ausgleichsgerade suchen, welche die Lage der über der Zeitachse aufgetragenen Temperaturen am besten wiedergibt. Die Temperaturdaten streuen allerdings mehr oder weniger stark um diese Gerade. Ein Maß dafür, wie nahe die Temperaturdaten auf der Gerade liegen, ist der Korrelationskoeffizient.

Fragen

Mit den monatlichen Mittelwerten

berechnen Sie bitte den Schwerpunkt und die Steigung der Ausgleichsgerade für die Wassertemperatur im Oktober 2002 - 2008. Zeichnen Sie ein Diagramm mit den Temperaturwerten über die Zeit, dem Schwerpunkt und der Ausgleichsgeraden.
berechnen Sie die gleichen Größen für die Daten in der Zeit Oktober 2002 - 2006, und tragen Sie das Ergebnis in das gleiche Diagramm ein.
berechnen Sie die Korrelationskoeffizienten der Daten jeweils für 2002 - 2008 und 2002 - 2006, und diskutieren Sie das Ergebnis.
vergleichen Sie die Wasser- und Lufttemperaturen für Oktober 2002 - 2008. Zeichnen Sie die Werte gegeneinander in ein Diagramm und berechnen Sie die Ausgleichsgerade und den Korrelationskoeffizienten.
vergleichen Sie die Daten der Wassertemperatur und des Salzgehalts für Oktober 2002 - 2008. Zeichnen Sie die Werte gegeneinander in ein Diagramm und berechnen Sie die Ausgleichsgerade und den Korrelationskoeffizienten. Wie interpretieren Sie die Ergebnisse?