Supplement 1.7: Stralingsgrootheden en radiometrie (4/9)

De stralingssterkte ... verder vanaf de vorige pagina

Voor een isotrope straler met richtingsonafhankelijke stralingssterkte kan de integraal worden opgelost. Bij een kegelvormige ruimtehoek zoals in de afbeelding in de linkerkolom van de vorige pagina, die echter in de richting van het zenit is georiënteerd, varieert de azimuthoek $φ$ van 0 tot $2 π$ . De zenithoek $ϑ$ varieert van 0 tot de halve openingshoek $ϑ'$ :

Φ = I \int_{ϑ = 0}^{ϑ'} \int_{φ = 0}^{2 π} sin ϑ d ϑ d φ = I \cdot 2 π (1 - cos ϑ')

Deze oplossing is een alternatief voor de berekening in het voorbeeld Efficiëntie van een lenscollimat op de vorige pagina.

Opdracht 2: Isotrope stralers ↓

Bij anisotrope stralers, waarvan de emissie symmetrisch is rond een as, kan de integraal gedeeltelijk worden opgelost. Hiervoor bekijken we de volgende grafiek, waarin een axiaal symmetrische ruimtehoek rond de verticale as (de zenitas) wordt weergegeven en eruitziet als een band rond de halve bol. Deze eveneens differentiële ruimtehoek is:

d Ω = \frac{d a}{R^{2}} = \int_{φ = 0}^{2 π} sin ϑ d ϑ d φ = 2 π sin ϑ d ϑ

Door aan te nemen dat de stralingssterkte $I (ϑ)$ alleen afhankelijk is van de zenithoek ϑ kan de emissie worden geïntegreerd over de azimuthoek φ:

Φ = \int_{ϑ_{1}}^{ϑ_{2}} \int_{φ = 0}^{2 π} I (ϑ) sin ϑ d ϑ d φ = 2 π \int_{ϑ_{1}}^{ϑ_{2}} I (ϑ) sin ϑ d ϑ

Vergelijkingen ↓

Integratie over de azimuthoek φ van 0 tot

2 π

resulteert in een band rond de bol onder de zenithoek ϑ met de breedte Rdϑ. Vanwege de differentiële breedte is ook deze band een differentiële oppervlakte-element da.

Opdracht 3: Anisotrope stralers ↓

De axiaal symmetrische stralingssterkte van een lamp wordt gegeven door

I (ϑ) = \frac{1}{2} I (ϑ = 0) (1 + cos ϑ)

Schets de verdeling van de stralingssterkte over de zenithoek ϑ van 0 tot 180°.
Bereken het totale uitgestraalde stralingsvermogen als functie van de stralingssterkte voor ϑ = 0.

Controleer uw resultaten op deze pagina!

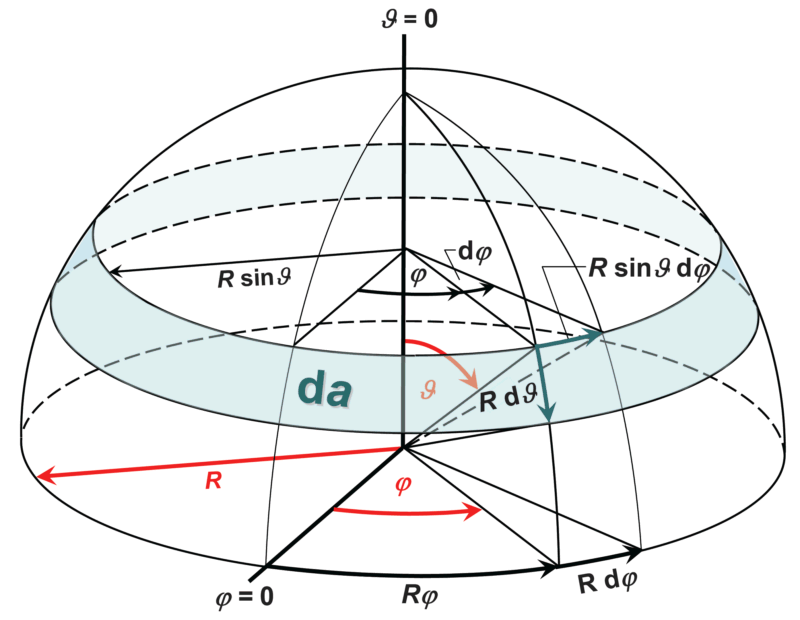
Een bijzondere vorm van anisotrope stralers zijn de cosinusstralers of Lambert-stralers, genoemd naar de wiskundige en natuurkundige Johann Heinrich Lambert (1728-1777). Deze stralers worden besproken in supplement 1.8.

Methoden voor het meten van de stralingssterkte worden beschreven in het gedeelte over radiantie.

Inzicht in Spectra van de Aarde

Supplement 1.7: Stralingsgrootheden en radiometrie (4/9)

De stralingssterkte ... verder vanaf de vorige pagina