5. Oefeningen

1.Licht en straling

Elektromagnetische golven (2/4)

Vraag: Tijdsverloop van zonlicht en maanlicht dat de aarde bereikt?

a) De afstand tussen de zon en de aarde is ongeveer 150·10⁶ km. Hoe lang duurt het (in seconden en minuten) voordat het licht van de zon de aarde bereikt?

b) De afstand tussen de maan en de aarde is 384 000 km, dus veel korter. Hoe lang duurt het voordat het zonlicht dat door het maanoppervlak wordt gereflecteerd de aarde bereikt?

Antwoord:

a) De tijd die het zonlicht nodig heeft om de aarde te bereiken is

of 8,33 minutes.

b) Voor het maanlicht is het

Vraag: Het lichtjaar en de afstand tot Alpha Centauri

De ster die het dichtst bij de zon staat heet Alpha Centauri. De afstand is opgegeven als 4,247 lichtjaar. Een lichtjaar is de afstand die het licht in één jaar aflegt, een lengte-eenheid die vaak in de sterrenkunde wordt gebruikt. Hoeveel kilometer is een lichtjaar? Hoe ver weg in kilometers is Alpha Centauri? Je zult je realiseren dat lichtjaren een heel praktische lengte-eenheid zijn om afstanden tot verre hemellichamen niet te onoverzichtelijk te maken!

Antwoord:

Een lichtjaar komt overeen met het product van de lichtsnelheid en de tijd 1 jaar, ofwel de tijd 365 dagen met elk 24 uur, 60 minuten en 60 seconden, ofwel 31,536·10⁶ seconden.

of 9,461·10¹² km of ongeveer 9,5 biljoen kilometer. De afstand van 4,247 lichtjaar tot Alpha Centauri komt overeen met ongeveer 40 biljoen kilometer.

Elektromagnetische golven (4/4)

Werkblat: Licht en Straling

Controleer en verdiep je kennis over het onderwerp van dit hoofdstuk met het werkblad Licht en straling. Het kan ook worden gebruikt als klassikale opdracht of als huiswerk.

Fotonen (4/4)

Taak: Een flits van 1000 fotonen

In het donker zien we de flits van een camera ver weg. We nemen aan dat 1000 fotonen van de flits het netvlies binnendringen via de pupil van ons oog, een echt heel zwakke lichtflits. In de linkerkolom hieronder staat dat een aan het donker aangepast oog deze flits waarschijnlijk net kan waarnemen.

De diameter van de pupil is 4 mm. De golflengte van het licht is 500 nm (een flits is dus eigenlijk wit). De flitsduur is 1 ms, wat overeenkomt met de flitsduur van fotoflitsen.

a) Bereken de energie van een enkel foton in elektronvolt en van de flits bestaande uit 1000 fotonen in joule.

b) De fotonen zijn gelijkmatig verdeeld over de duur van de flits. Wat is het momentane vermogen dat door de pupil gaat?

c) Wat is de bestralingssterkte in W/m² van de flits op onze plaats?

Antwoorden:

a) De energie van een foton is:

1 J komt overeen met 1,6·10^-19 eV. Dit wordt: E = 2,48 eV. Vergelijk het resultaat met het diagram op pagina Fotonen (3/4).

De totale energie van de 1000 fotonen van de bliksem in het oog is 0,4·10^-15 J of 0,4 fJ.    (10^-15 = 1 quadriljoenste = 1 femto, afkorting f)

b) De energie van de flits duurt één milliseconde. Het vermogen door de pupil tijdens de flitsduur is:

of 0,4 pW.    (10^-12 = 1 biljoenste = 1 pico, afkorting p)
Het is moeilijk te geloven dat het oog zo'n bliksem kan zien!

c) De straal van de pupil is r = 2 mm. Het doorgelaten vermogen is 0,4·10^-12 W. De bestralingssterkte is dus:

of 32 nW/m². Ter vergelijking: Bij een onbewolkte hemel is de bestralingssterkte op de grond bij volle maan ongeveer 3 mW/m², de zon op het zenit straalt met ongeveer 1 kW/m².

Spectraalanalyse: Filters van gekleurd glas (4/4)

Oefening: Reflecties

Vergelijk de zwart-witafbeeldingen van band 1 tot 4 met de valse kleurenafbeelding.

1. Evalueer de reflecties van begroeide en niet-begroeide landoppervlakken en van het zeewater op basis van hun helderheid.
2. Kijk eens naar de tabel met TM-banden op de vorige pagina. Kunt u de beschrijvingen onder kolom kenmerken?
3. Onderzoek je bevindingen verder door ze te vergelijken met informatie op gerelateerde SEOS-pagina's op
• spectroscopische kenmerken van vegetatie in tutorial Teledetectie en GIS in de landbouw
• spectroscopische kenmerken van zeewater in de tutorial Zeekleur
• classificatie van satellietbeelden in tutorial Classification Algorithms and Methods

Voor deze opdracht worden geen antwoorden voorgesteld.

 

Supplement 1.1: De vergelijkingen van Maxwell

Vraag 1: Divergentie en kromming van een vector

Toon aan dat de hierboven opgegeven vergelijkingen voor de divergentie $\nabla \cdot \overrightarrow{E}$ en de kromming $\nabla \times \overrightarrow{E}$ van de vector van het elektrisch veld correct zijn. Zijn deze termen scalaire grootheden of vectoren?

Antwoord:

is een scalair,

is een vector. $i$, $j$ en $k$ zijn de eenheidsvectoren in de richting van de $x$-, $y$- en $z$-coördinaten.

Vraag 2: Gradiënt van een scalaire grootheid

Om volledig te zijn kan de ∇-operator verder toegepast worden met scalaire grootheden. Laat $\phi (x,y,z)$ een scalaire functie in de ruimte zijn, bv. het elektrisch potentiaal. De term ∇φ geeft dan de ruimtelijke afgeleide van φ, ook wel grad φ genoemd. ∇φ is een vector aangezien vector ∇ vermenigvuldigd wordt met de scalair φ.

Gelieve ∇φ in componenten in de x-, y-, en z-richtingen te schrijven.

Antwoord:

Supplement 1.2:
De vergelijkingen van Maxwell oplossen voor elektromagnetische golven

Vraag 1: De Laplace-operator

In cartesiaanse coördinaten is de nabla-operator

de ruimtelijke afgeleide van de eerste orde. Het scalaire product $\nabla \cdot \nabla =\Delta$ is dan de ruimtelijke afgeleide van de tweede orde, de Laplace-operator.

a) Toon aan dat de Laplace-operator in cartesiaanse coördinaten is:

b) Schrijf de golfvergelijking van het elektrisch veld op in zijn componenten in cartesiaanse coördinaten.

Antwoord:

a)     $\nabla \cdot \nabla =\Delta =\left(\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial x}\right)\cdot \left(\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial x}\right)=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}$

b) Voor het elektrische veld $\overrightarrow{E}=\left(E_x,E_y,E_z\right)$ van een golf in elke richting is de x-component:

en overeenkomstig voor de y- en z-componenten en de componenten van het magnetische veld.

Vraag 2: Derde vergelijking van Maxwell in cartesiaanse componenten

Toon door berekening aan dat de veldvectoren

toegepast op de derde vergelijking van Maxwell, de componenten geven:

Antwoord:

De derde vergelijking van Maxwell

In componenten:

De bewering volgt hieruit.

Supplement 1.4:
Energiedichtheid en bestralingssterkte van elektromagnetische golven

Vraag 1: Energie en intensiteit van elektromagnetische golven

Hoofdstuk 2 Temperatuurstraling laat zien dat de stralingssterkte van zonnestraling aan de buitenrand van de aardatmosfeer 1361 W/m² is, wat bekend staat als de zonneconstante. Bereken de elektrische en magnetische veldsterkte van deze straling.

Antwoord:

Met $c=3\cdot {10}^8\text{m}/\text{s}$, ${\epsilon }_o=\mathrm{8<mo>,</mo>854}\cdot {10}^{-12}\frac{\text{A}\text{s}}{\text{V}\text{m}}$ en ${\mu }_o=\mathrm{1<mo>,</mo>26}\cdot {10}^{-6}\frac{\text{V}\text{s}}{\text{A}\text{m}}$ volgt:

Het elektrische veld is heel sterk, het magnetische veld heel klein. De oorzaak is - zoals te zien is in het supplement - de relatie $E=cB$. De veldenergieën van het elektrische en magnetische veld zijn echter hetzelfde.

De amplitude van een vlakke monochromatische golf wordt hier berekend, wat niet van toepassing is op zonnestraling met zijn brede spectru. De numerieke waarden van het resultaat zijn desondanks geldig, omdat spectrale eigenschappen niet zijn meegenomen in de berekening van de veldsterktes.

Supplement 1.6: Stralingsdruk

Opdracht 1: De stralingsdruk van zonnestraling

1. Hoofdstuk 3, paragraaf Klimaat en klimaatverandering, laat zien dat de bestralingssterkte van zonnestraling aan de buitenrand van de aardatmosfeer 1361 W/m² is; dit is de zogenaamde zonneconstante. Hoe groot is de stralingsdruk van zonnestraling?
   
   Antwoord:
   
   Het geldt:            $p_{rad}=\frac{E_{rad}}{c}$
   
   met $c=3\cdot {10}^8\text{m}/\text{s}$ en $E_{rad}=1361\text{W}/{\text{m}}^{\text{2}}$ je krijgt:
   $p_{rad}=\mathrm{4<mo>,</mo>54}\cdot {10}^{-6}\text{Ws}/{\text{m}}^{\text{3}}=\mathrm{4<mo>,</mo>54}\cdot {10}^{-6}{\text{N<mo>/</mo>m}}^{\text{2}}=\mathrm{4<mo>,</mo>54}\text{<mo>µ</mo>Pa}$
2. Verminderd door absorptie en verstrooiing door de luchtmoleculen bereikt ongeveer 65% van de zonnestraling die aanwezig is aan de buitenrand van de atmosfeer het aardoppervlak op een wolkenvrije dag. Vergelijk de stralingsdruk hier met de luchtdruk op zeeniveau, die gemiddeld 1013 hPa bedraagt.
   
   Antwoord:
   
   65% van de stralingsdruk aan de buitenrand van de atmosfeer resulteert in $p_{rad}=\mathrm{2<mo>,</mo>95}\text{<mo>µ</mo>Pa}$ aan het aardoppervlak. De standaard luchtdruk van 1013 hPa is 34·10⁹ keer zo hoog als deze stralingsdruk. De stralingsdruk speelt dus geen rol bij mechanische processen aan het aardoppervlak.


3. De specifieke straling van de fotosfeer van de zon wordt ook berekend in hoofdstuk 3, paragraaf Klimaat en klimaatverandering. De fotosfeer is het gebied van de zonneatmosfeer waarin de zonnestraling die de ruimte in wordt gestuurd, wordt opgewekt. Deze bedraagt 62,9 MW/m². Wat is de waarde van de stralingsdruk daar?
   
   Antwoord:
   
   De overeenkomstige berekening resulteert in $p_{rad}=\mathrm{0<mo>,</mo>21}\text{Pa}$. De gasdruk van de fotosfeer van de zon is 0,87 hPa aan de bovenrand en 125 hPa aan de onderrand. Ook hier speelt de stralingsdruk slechts een ondergeschikte rol.


4. Ruimtevaartorganisaties onderzoeken hoe stralingsdruk kan worden gebruikt om ruimtevaartuigen voort te stuwen. Hoewel de versnelling die haalbaar is met een reflecterend zonnezeil te laag is voor bemande ruimtevluchten, zou het langetermijnmissies van kleine onbemande satellieten mogelijk moeten maken zonder extra voortstuwing.
   Een uitdaging is het ontwikkelen van materialen voor lichtgewicht maar robuuste zeilen en de mechanische structuren om ze in de ruimte in te zetten. NASA's laatste poging (laatste oproep: 16 april 2025) is om een sonde met een totale massa van 16 kg voort te stuwen met behulp van een zeil van 80 m². De baan van de aarde moet gesynchroniseerd zijn met de zon zodat de zon het zeil altijd verticaal verlicht met de zonneconstante van 1361 W/m². Bereken de haalbare versnelling.
   
   Antwoord:
   
   Het is       $F=ma=p_{rad}A=\left(1+r\right)\frac{E_{rad}A}{c}$
   met het zeiloppervlak $A=80{\text{m}}^{\text{2}}$ en een ideaal reflecterend zeil met de reflectiecoëfficiënt $r=1$, en met de massa $m=16\text{kg}$ van de satelliet. De versnelling resulteert in
   $a=\left(1+r\right)\frac{E_{rad}A}{mc}=\mathrm{72<mo>,</mo>6}\cdot {10}^{-6}\frac{\text{m}}{{\text{s}}^{\text{2}}}$,
   een vrij kleine waarde. Toch is de snelheid na één dag (na 86400 seconden) met 6,27 m/s veranderd.

Werkblad 1.2: Komeetstaarten

Vul je kennis over stralingsdruk aan met werkblad 1.2: Komeetstaarten.

Taken: Komeetstaarten

1. Bereken de verhouding tussen de zwaartekracht en de stralingsdruk. Wat is de afhankelijkheid van het quotiënt van de dichtheid, de diameter en de afstand tot de zon?
   
   Oplossing:
   
   
   $F_{rad}=\mathrm{80<mo>,</mo>7}\cdot {10}^{15}\text{N}\cdot \frac{d^2}{R^2}$
   $F_{grav}=\mathrm{69<mo>,</mo>5}\cdot {10}^{18}\frac{\text{N}\cdot {\text{m}}^{\text{2}}}{\text{kg}}\frac{\rho d^3}{R^2}$
   $\frac{F_{grav}}{F_{rad}}=869\rho d\frac{{\text{m}}^{\text{2}}}{\text{kg}}$
   De verhouding is evenredig met de dichtheid en de deeltjesgrootte. De afstand tot de zon is niet belangrijk.
2. Kleine ijskristallen in de staart van de komeet hebben de dichtheid van water, dus ongeveer 1000 kg/m³. Voor welke deeltjesdiameter heffen de stralingsdruk en de zwaartekracht elkaar op? Klopt de hypothese dat kleine deeltjes worden afgestoten door de stralingsdruk en grote deeltjes worden aangetrokken door de zon?
   
   Oplossing:
   
   
   $\rho =1000\frac{\text{kg}}{{\text{m}}^{\text{3}}}\to \frac{F_{grav}}{F_{rad}}=869\cdot {10}^{3}d$
   $d=\mathrm{1<mo>,</mo>15}\cdot {10}^{-6}\text{m}=\mathrm{1<mo>,</mo>15}\text{<mo>µ</mo>m}$ voor $\frac{F_{grav}}{F_{rad}}=1$
   De hypothese is juist. De kritische grootte van absorberende deeltjes waarbij beide krachten gelijk zijn, is ongeveer 1 µm.
3. De deeltjes in komeetstaarten zijn duidelijk eerder reflecterend dan absorberend. Hoe verandert de diameter waarbij de twee krachten gelijk zijn voor ideaal reflecterende deeltjes?
   
   Oplossing:
   
   De kracht die door de stralingsdruk wordt uitgeoefend op ideaal reflecterende deeltjes verdubbelt, terwijl de zwaartekracht gelijk blijft. De kritische deeltjesgrootte wordt dus gehalveerd.

Supplement 1.7:: Stralingsgrootheden en radiometrie

Opdracht 1: De stralingsintensiteit van de zon

Het totale stralingsvermogen van de zon is 387,5·10²⁴ W. De straling is isotroop gericht in de ruimte. De afstand tussen de zon en de aarde is 149 589 000 km ((de zogenaamde astronomische eenheid, AU). Vanwege deze grote afstand kunnen we de zon vanaf de aarde bij benadering als een puntlichtbron beschouwen. De straal van de aarde is 6371 km.

1. Wat is de waarde van de stralingssterkte van de zon in de hele ruimte? Welke stralingssterkte treft de aarde in totaal, respectievelijk een vierkante meter van de aarde?
   
   Oplossing:
   

   De stralingssterkte $I_S$ van het zonneoppervlak is:

   $I_S=\frac{{\Phi }_S}{{\Omega }_{4\pi }}=\frac{\text{387}\text{<mo>,</mo>5}\cdot {\text{10}}^{\text{24}}\text{W}}{4\pi \text{sr}}=\mathrm{30<mo>,</mo>84}\cdot {10}^{24}\frac{\text{W}}{\text{sr}}$

   Voor een isotrope straler is de stralingssterkte constant, de stralingsvermogen verandert dus evenredig met de ruimtehoek. De stralingssterkte die de aarde als geheel treft en de stralingssterkte voor een vierkante meter van de aarde hebben daarom dezelfde waarde als de stralingssterkte van de zon in de ruimte.

2. Bereken de ruimtehoek waaronder de aarde vanaf de zon verschijnt. Hoe groot is het stralingsvermogen dat op de aarde valt?
   
   Oplossing:
   

   Met de gegevens voor de straal van de aarde en de afstand van de aarde tot de zon volgt voor de ruimtehoek ${\Omega }_{S\to E}$, waaronder het dwarsdoorsnedeoppervlak van de aarde vanaf de zon verschijnt:

   ${\Omega }_{S\to E}=\frac{\pi {\left(\mathrm{6<mo>,</mo>371}\cdot {10}^6\right)}^2}{{\left(\mathrm{149<mo>,</mo>589}\cdot {10}^9\right)}^2}=\mathrm{5<mo>,</mo>70}\cdot {10}^{-9}\text{sr}$

   Vanwege de isotrope aard van zonnestraling geldt:

   $I_S=\frac{{\Phi }_S}{{\Omega }_{4\pi }}=\frac{{\Phi }_{S\to E}}{{\Omega }_{S\to E}}=I_{S\to E}$

   Voor de stralingsvermogen ${\Phi }_{S\to E}$ die op de dwarsdoorsnede van de aarde valt, geldt:

   ${\Phi }_{S\to E}=I_S\cdot {\Omega }_{S\to E}=\mathrm{175<mo>,</mo>5}\cdot {10}^{15}\text{W}$
3. Bereken de ruimtehoek waaronder een vierkante meter van de aarde vanaf de zon verschijnt, evenals de stralingsenergie die op een vierkante meter van de aarde valt. Vergelijk het resultaat met de in hoofdstuk 3 opgegeven zonneconstante, die overeenkomt met de stralingsintensiteit aan de buitenrand van de aardatmosfeer.
   
   Oplossing:
   

   De ruimtehoek voor een vierkante meter van het aardoppervlak is:

   ${\Omega }_{S\to 1{\text{m}}^2}=\frac{1}{{\left(\mathrm{149<mo>,</mo>589}\cdot {10}^9\right)}^2}=\mathrm{44<mo>,</mo>69}\cdot {10}^{-24}\text{sr}$

   Het geldt opnieuw:

   $I_S=\frac{{\Phi }_S}{{\Omega }_{4\pi }}=\frac{{\Phi }_{S\to 1{\text{m}}^2}}{{\Omega }_{S\to 1{\text{m}}^2}}=I_{S\to 1{\text{m}}^2}$

   Het stralingsvermogen wordt:

   ${\Phi }_{S\to 1{\text{m}}^2}=I_S\cdot {\Omega }_{S\to 1{\text{m}}^2}=1378\text{W}$

   De zonneconstante is 1361 W/m². Binnen de nauwkeurigheid van deze schatting is de overeenstemming vrij goed.

Opdracht 2: Isotrope stralers

1. Vergroot de ruimtehoek van de naar het zenit gerichte kegel tot een halve bol (of: tot een halve ruimte). Wat is dan het verband tussen stralingsvermogen en stralingssterkte?
   
   Oplossing:
   

   Bij een kegelvormige ruimtehoek, gericht in de richting van het zenit, varieert de azimuthoek $\phi$ van 0 tot $2\pi$. De zenithoek $\vartheta$ varieert van 0 tot de halve openingshoek $\vartheta \text{'}$:

   $\Phi =I\underset{\vartheta =0}{\overset{\vartheta \text{'}}{\int }}\underset{\phi =0}{\overset{2\pi }{\int }}sin\vartheta \text{d}\vartheta \text{d}\phi =I\cdot 2\pi \left(1-cos\vartheta \text{'}\right)$

   Voor $\vartheta \text{'}=\pi /2$ geldt $\Phi =2\pi I$.

2. Vergroot de ruimtehoek verder tot de hele ruimte en bereken opnieuw het verband.
   
   Oplossing:
   

   Voor $\vartheta \text{'}=\pi$ geldt $\Phi =4\pi I$. Dit resultaat werd al aan het begin van het gedeelte over de stralingssterkte gevonden.

Opdracht 3: Anisotrope stralers

De axiaal symmetrische stralingssterkte van een lamp wordt gegeven door

1. Schets de verdeling van de stralingssterkte over de zenithoek ϑ van 0 tot 180°.
   
   Oplossing:
   
   

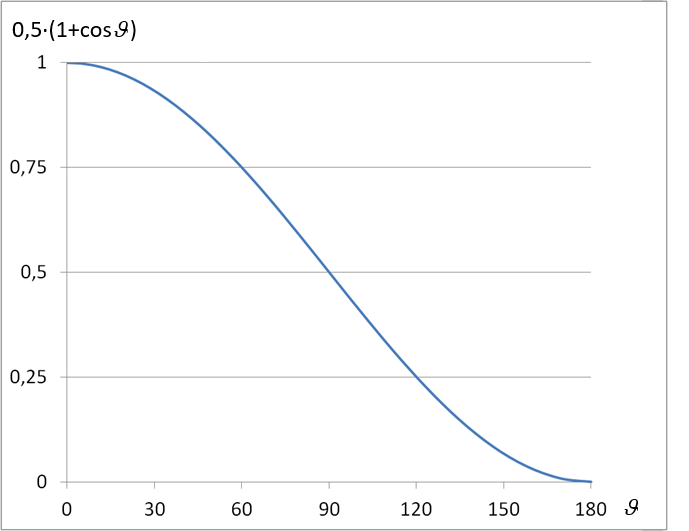   Stralingssterkte van de anisotrope straler afhankelijk van de zenithoek ϑ.
2. Bereken het totale uitgestraalde stralingsvermogen als functie van de stralingssterkte voor ϑ = 0.
   
   Oplossing:
   $\begin{array}{c}\Phi =2\pi \underset{0}{\overset{\pi }{\int }}I\left(\vartheta \right)sin\vartheta \text{d}\vartheta \\ =\pi I\left(0\right)\underset{0}{\overset{\pi }{\int }}(1+cos\vartheta )sin\vartheta \text{d}\vartheta \\ =\pi I\left(0\right)\left\{{\left[-cos\vartheta \right]}_0^{\pi }+{\left[\frac{1}{2}{sin}^2\vartheta \right]}_0^{\pi }\right\}\\ =\pi I\left(0\right)\left\{2+0\right\}\\ =2\pi I\left(0\right)\end{array}$

Supplement 1.8:: Lambert-straler, cosinusstraler

Opdracht 1: Het stralingsvermogen van cosinusstralers

Een belangrijke groep anisotrope axiaal symmetrische stralers zijn de cosinusstralers. Hun stralingssterkte neemt af met toenemende zenithoek ϑ in het bereik van 0 tot $\pi /2$ overeenkomstig cos ϑ:

Bereken het stralingsvermogen van een cosinusstraler in een kegelvormige ruimtehoek met de maximale zenithoek ϑ' en het stralingsvermogen in de bovenste halve ruimte.

Oplossing:

De stralingsvermogen tot de hoek ϑ':

Het stralingsvermogen in het bovenste halve ruimte: