Ergänzung 1.7: Strahlungsgrößen und Radiometrie      (2/7)

 

Spektrale Größen

Spektrale Eigenschaften zu berücksichtigen ist für alle Strahlungsgrößen fast immer erforderlich. Dies geschieht mit Differenzialquotienten und mit den Indizes f für die Frequenz bzw. λ für die Wellenlänge. Am Beispiel der Strahlungsleistung wird dies folgendermaßen geschrieben:

Φ f = dΦ df     mit     [ Φ f ]= W Hz
Φ λ = dΦ dλ     mit     [ Φ λ ]= W m

Oft ist es zweckmäßig, Leistungen in mW, kW oder MW anzugeben, um praktikable Zahlenwerte zu erhalten. Gleiches gilt für Frequenzen und für Wellenlängen, die in kHz, MHz bzw. in nm, µm oder mm angegeben werden können. Für die Umrechnung von Größen, die auf Wellenlängen bezogen sind, zu frequenz­bezogenen Größen und umgekehrt gilt:

Φ f = λ 2 c Φ λ     und     Φ λ = f 2 c Φ f

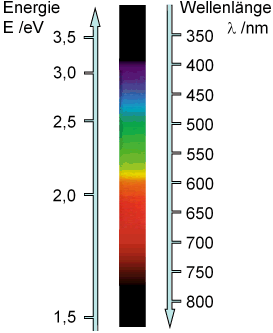
Die Größe c ist die Lichtgeschwindigkeit. Der Beweis findet sich auf einer Seite zum Thema Plancksches Strahlungs­gesetz in der Frage: Wie rechnet man um von Frequenzen nach Wellenlängen? Wegen der quadratischen Ausdrücke in λ und f ist der Zusammenhang nichtlinear. Dies erkennt man beispielsweise im Spektrum des sichtbaren Lichts, das linear über die Wellenlänge, aber nichtlinear über die Photonenenergie E=hf dargestellt ist.

Gleichungen ↓

Die Strahlungsenergie (engl.: radiant energy)

Die Strahlungsenergie entspricht der zeitlichen Integration der Strahlungs­leistung. Umgekehrt ist die Strahlungsleistung gleich der zeitlichen Ableitung der Strahlungsenergie:

Q=∫ Φ dt        Φ= dQ dt

Formelzeichen: Q
Maßeinheit: Joule, [ Q ]=J

Der Parameter ist für beispielsweise die Photosynthese der Vegetation von Bedeutung, oder auch für die Ausbeute der Photovoltaik in Regionen mit unterschiedlichen Sonnenscheindauern.

Das Formelzeichen Q ist der Thermodynamik entlehnt; dort bezeichnet es eine Wärmemenge. Das in der Mechanik für die kinetische Energie gängige Zeichen E ist für die Strahlungsenergie nicht sinnvoll, da E in der Radiometrie vielfach für die Bestrahlungsstärke genutzt wird. In der Quantenphysik bedeutet E die Photonenenergie. In der Ergänzung 1.6 über den Strahlungsdruck kommt sowohl die Photonenenergie als auch die Bestrahlungsstärke vor; zur Unterscheidung wird in SEOS daher das Formelzeichen E rad für die Bestrahlungsstärke genutzt.